컴퓨터 구조 - 2-4. 데이터의 표현(논리 게이트, 부울 대수, 카노 맵)
이 포스트는 패스트캠퍼스의 “컴퓨터 공학 전공 필수 올인원 패키지 Online.” 강의를 보고 정리한 내용입니다.
데이터의 표현
컴퓨터에서 데이터를 표현하는 방법에 대해서 알아보자.
1. 논리 게이트(Logical Gate)
사칙연산 같은 산술 연산이 아닌 논리 연산을 수행하는 전자 소자가 논리 게이트이다.
논리 게이트는 입력 변수가 주어지면 정해진 논리 함수를 수행하고 그 결과값과 동일하게 출력하는 하드웨어이다.
1-1. 스위칭 이론
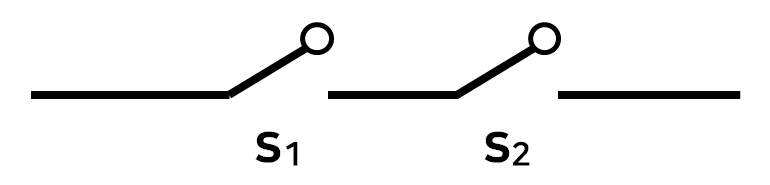
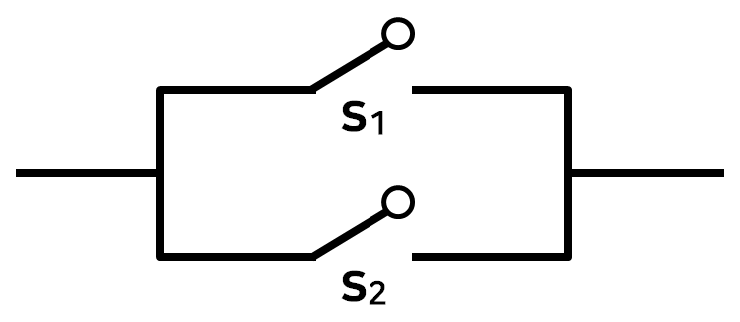
1983년 미국의 샤논(C.E. Shannon)이 스위치(power on/off)로 2진 정보를 표현하거나 논리 연산의 실행을 가능하도록 구성된 이론을 만들었다.
1) 2진 정보의 표현 기능
2) 논리적 연산 기능
1-2. 논리 연산의 기본 표현
컴퓨터의 메인보드와 칩의 내부에서 사용되는 논리 연산들의 기본 표현들이 있다.
이러한 논리 연산들의 정보를 3가지 방식으로 알아보자.
- 진리 표(Truth Table): 논리 연산의 모든 입력과 출력의 결과를 정리한 표
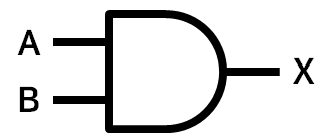
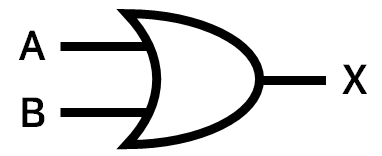
- 심볼(Symbol): 논리 게이트를 간단하게 그릴 수 있는 유일한 형태
- 대수적 표현(Algebraic Expression): 대수적 형태로 표현
1) 논리곱(AND)
| 진리표 | ||
|---|---|---|
| 입력(A) | 입력(B) | 출력(X) |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
대수적 표현 : $X = A \cdot B$
2) 논리합(OR)
| 진리표 | ||
|---|---|---|
| 입력(A) | 입력(B) | 출력(X) |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
대수적 표현 : $X = A + B$
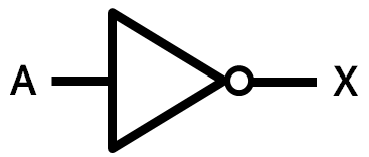
3) 논리부정(NOT)
| 입력(A) | 출력(X) |
|---|---|
| 0 | 1 |
| 1 | 0 |
대수적 표현 : $X = \overline{A}$
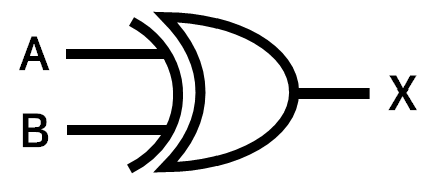
4) 배타적 논리합(XOR;Exclusive OR)
| 입력(A) | 입력(B) | 출력(X) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
대수적 표현 : $\begin{flalign}& X = A \oplus B \cr & X = A\overline{B} + \overline{A}B \end{flalign}$
1-3. 실무 적용 사례
위의 논리 회로들이 만들어지고 실무에 적용된 사례를 살펴보자.
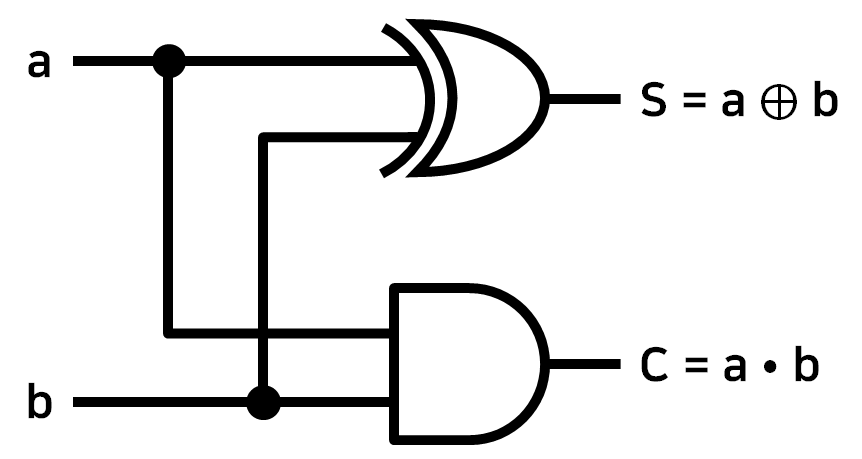
1) 1bit 덧셈(반 가산기)
논리 회로를 이용한 반 가산기(Half Adder)를 구현했다.
a + b = S 라는 기본 연산을 구현한다고 가정하자.
그 과정은 다음과 같다.
- 단일 비트에 의한 연산 결과의 예측값으로 진리 표를 구한다.(C: Carry bit)
- 진리표
a b C S 0 0 0 0 0 1 0 1 1 0 0 1 1 1 1 0 - 진리 표의 값을 구현할 수 있는 부울 대수식을 구현한다.
- $\begin{flalign}&S = a’b + ab’ = a \oplus b \cr &C = a \cdot b \end{flalign}$
- 위 정보를 기반으로 Symbol 을 사용해 회로를 구성
2. 부울 대수(Boolean Algebra)
위에 정리한 샤넌의 스위치 이론을 수학적인 형태로 변환시키기 위해 사용된 개념이 부울 대수이다.
부울 대수는 산술 연산처럼 논리 연산을 수리적으로 표현할 수 있게 만들어진 개념이다.
1854년 영국의 수학자 부울(G.Boole)이 참 / 거짓 을 판별할 수 있는 논리적 명제를 수학적인 표현의 논리전개 식으로 구현했다.
이러한 부울 대수는 다음과 같은 특징을 가진다.
- 논리 회로의 형태와 구조를 기술하는데 필요한 수학적인 이론이다.
- 변수들의 진리 표 관계를 대수식으로 표현하기 용이하다.
- 같은 성능의 회로를 더 간단히 만들기 용이하다.
2-1. 부울 대수의 기본 법칙
산술연산에서 사용되던 다양한 법칙들처럼 다양한 법칙들이 존재하고, 산술연산의 법칙과 비슷한 면도 있다.
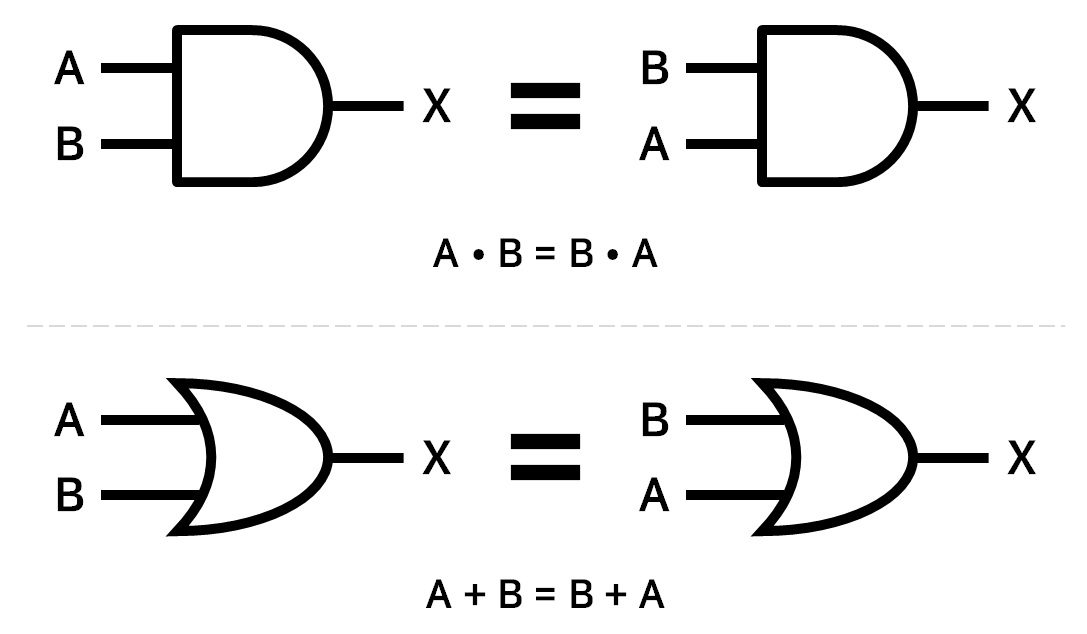
1) 교환법칙(Commutative Law)
부울 대수식
먼저 부울 대수로 표현하면 다음과 같다.
- $A \cdot B = B \cdot A$
- $A + B = B + A$
연산에 대해 입력 변수들의 순서가 바뀌어도 결과는 동일하다는 의미이다.
심볼과 진리표
심볼과 진리표는 다음과 같다.
| $A$ | $B$ | $A \cdot B$ | $B \cdot A$ | $A + B$ | $B + A$ |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 |
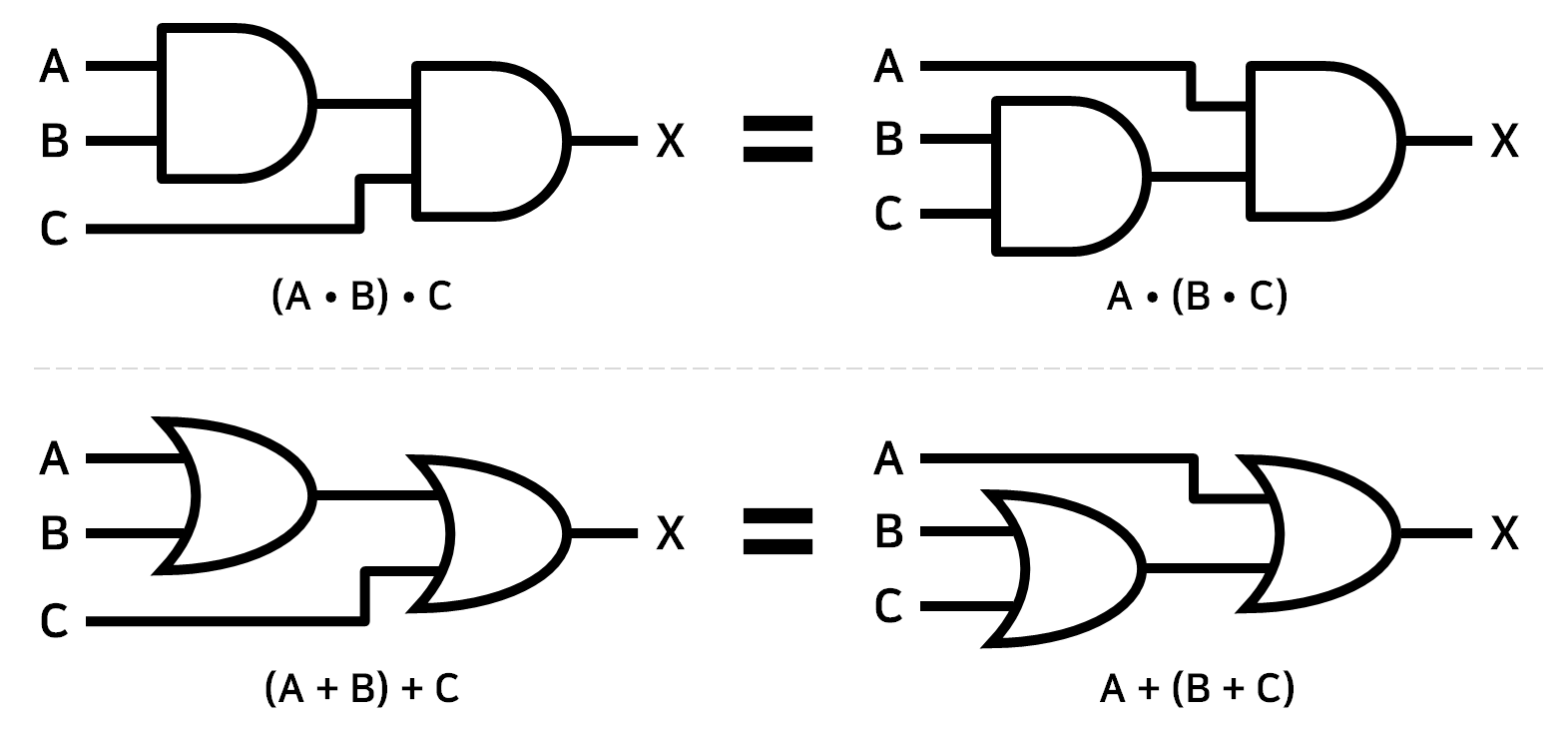
2) 결합법칙(Associative Law)
부울 대수식
- $A \cdot (B \cdot C) = (A \cdot B) \cdot C$
- $(A + B) + C = A + (B + C)$
심볼과 진리표
| $A$ | $B$ | $C$ | $(A \cdot B) \cdot C$ | $A \cdot (B \cdot C)$ | $(A + B) + C$ | $A + (B + C)$ |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 |
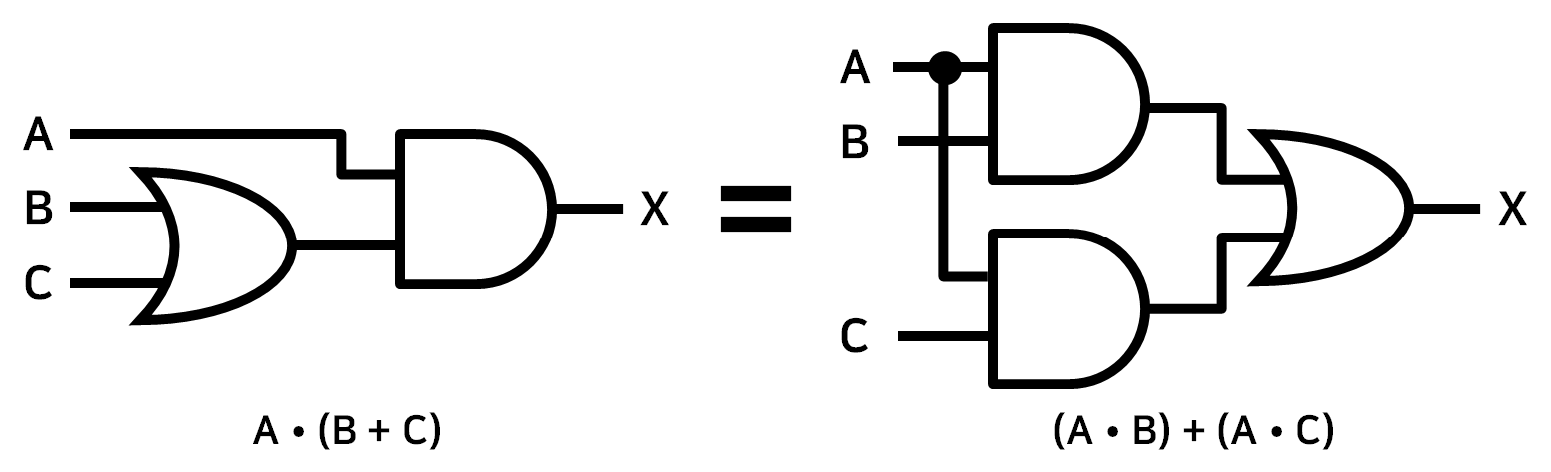
3) 분배법칙(Distributive Law)
부울 대수식
- $A \cdot (B + C) = A \cdot B + A \cdot C$
심볼과 진리표
| $A$ | $B$ | $C$ | $A \cdot (B + C)$ | $(A \cdot B) + (A \cdot C)$ |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 |
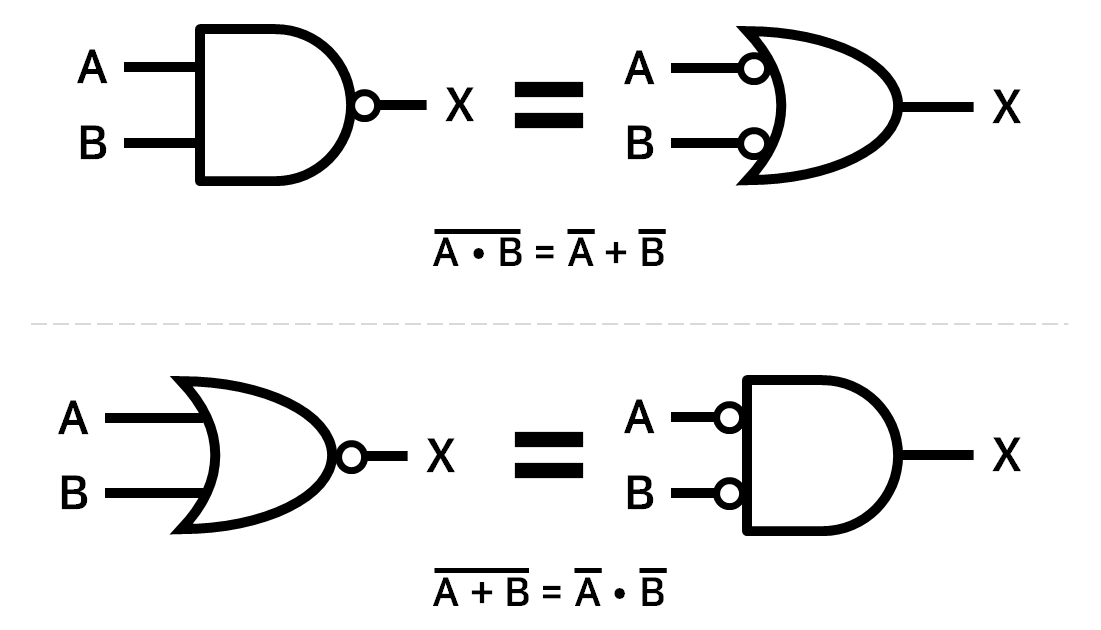
4) 드모르간의 정리(De Morgan’s Theorem)
부울 대수식
- $\overline{A + B} = \overline{A} \cdot \overline{B}$
- $\overline{A \cdot B} = \overline{A} + \overline{B}$
심볼과 진리표
| $A$ | $B$ | $\overline{A}$ | $\overline{B}$ | $\overline{A \cdot B}$ | $\overline{A} + \overline{B}$ | $\overline{A + B}$ | $\overline{A} \cdot \overline{B}$ |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
2-2. 부울 대수를 이용한 간략화
부울 대수의 기본 법칙들을 활용하면 부울식을 간략화 할 수 있다.
간단한 예시로 다음 부울식을 간략화 해보자.
$E = (a’ + bc)(a + b)$
위 식을 간략화 하시오.
풀이
간략화 과정은 다음과 같다.
\[\begin{flalign} E &= (a' + bc)(a + b) \\ &= aa' + a'b + abc + bbc \qquad\, (1) \\ &= a'b + abc + bc \qquad\qquad\;\;\;\; (2) \\ &= (a + 1)bc + a'b \qquad\qquad\;\;\, (3) \\ &= bc + a'b \qquad\qquad\qquad\quad\;\;\, (4) \end{flalign}\]- 분배 법칙을 사용해 풀어준다.
- 4개 항 중 $aa’$ (a AND NOT(a)) 는 무조건 False 이므로 생략이 가능하다.
또한, $bc \cdot b$ 는 분배법칙에 의해 $(b \cdot b) \cdot c = bc$ 가 된다. - 분배 법칙을 사용해 뒤 2개 항을 묶어준다.
- 묶인 항의 $(a + 1)$ 은 무조건 True 이므로 생략이 가능하다.
따라서 간략화된 최종 식은 $bc + a’b$ 가 된다.
이와 같이 복잡한 식을 간략화 하기 위해 부울 대수를 사용한다.
3. 카노 맵(Karnaugh Map)
위에서 부울 대수의 법칙을 활용해 표현식을 간략화해보았는데, 이는 여러 법칙을 사용한 방식이었다.
반면 카노 맵을 활용한 맵 방법은 부울 함수를 곧바로 간소화 할 수 있어 널리 활용된다.
이러한 카노 맵은 깊게 파고들면 많은 내용을 알아야 하지만 간단하게 사용하는 이유와 방법만 알아보자.
3-1. 카노 맵의 표현
카노 맵은 입출력의 진리표를 바탕으로 표현식의 간편화를 위해 그려지는 표 형태의 맵이다.
이러한 카노 맵을 표현할 때는 다음과 같은 규칙을 지켜야 한다.
1. 변수가 n개 이면 카노 맵은 $2^n$개의 민텀(minterm)으로 구성된다.
이해를 위해 변수의 개수에 따른 카노 맵의 구성을 미리 살펴보자.
변수가 2개인 경우
변수 b b’ a ab ab’ a’ a’b a’b’ 변수가 3개인 경우
변수 bc b’c b’c’ bc’ a abc ab’c ab’c’ abc’ a’ a’bc a’b’c a’b’c’ a’bc’ 변수가 4개인 경우
변수 cd c’d c’d’ cd’ ab abcd abc’d abc’d’ abcd’ a’b a’bcd a’bc’d a’bc’d’ a’bcd’ a’b’ a’b’cd a’b’c’d a’b’c’d’ a’b’cd’ ab’ ab’cd ab’c’d ab’c’d’ ab’cd’
위의 표 형태가 카노 맵이고, 첫번째 행과 열을 제외한 내부의 값들이 민텀(minterm)이다.
이 민텀은 minterm expansion(최소항 전개) 에서 비롯된 개념인데, minterm expansion 은 논리 함수의 모든 변수가 곱의 합 형태로 표현된 형태를 말한다.
예를들어 $E = a(b + c) + bc$ 는 분배 법칙으로 전개가 가능하므로 minterm expansion 이 아니다. 분배된 후의 식인 $E = ab + ac + bc$ 가 바로 minterm expansion 이 된다.
이러한 minterm expansion 에서 나올 수 있는 모든 곱 형태의 항들은 카노 맵 내부의 민텀(최소항)들의 값으로 표현될 수 있으며, 변수의 개수가 늘어남에 따라 카노 맵이 나타내는 민텀의 개수가 $2^n$ 개로 늘어난다.
2. 인접한 민텀들 간에는 하나의 변수만이 변경되어야 한다.
위의 예시 카노 맵 중 하나를 보자.
| 변수 | cd | c’d | c’d’ | cd’ |
|---|---|---|---|---|
| ab | abcd | abc’d | abc’d’ | abcd’ |
| a’b | a’bcd | a’bc’d | a’bc’d’ | a’bcd’ |
| a’b’ | a’b’cd | a’b’c’d | a’b’c’d’ | a’b’cd’ |
| ab’ | ab’cd | ab’c’d | ab’c’d’ | ab’cd’ |
위 표 형태의 카노 맵에서 인접하다는 의미는 바로 옆 행이나 열이라는 것을 의미한다.
결국 바로 옆 행 혹은 바로 옆 열 민텀들 사이의 차이점은 4개의 변수중 딱 1개만 존재한다는 뜻이다.
이러한 특성 때문에 첫번째 행과 열의 변수의 순서가 0, 1, 2, 3 순서가 아닌 0, 1, 3, 2 순서로 배치가 된다.
(ex. ab, a’b, a’b’, ab’ = 00, 01, 11, 10 이런 식.)
따라서 이러한 순서로 위 카노 맵을 다시 표현하면 다음과 같은 순서가 된다.
| 변수 | cd | c’d | c’d’ | cd’ |
|---|---|---|---|---|
| ab | 0 | 1 | 3 | 2 |
| a’b | 4 | 5 | 7 | 6 |
| a’b’ | 12 | 13 | 15 | 14 |
| ab’ | 8 | 9 | 11 | 10 |
3. 출력이 1인 기본 곱에 해당하는 민텀은 1로, 나머지는 0으로 표시한다.
이 내용은 뒤에서 실제 예시를 보면서 이해를 해보자.
3-2. 카노 맵을 이용한 간편화
이제 위의 규칙을 따라 만들어진 카노 맵을 사용해 부울 식을 간편화 해보자.
이전처럼 부울 대수의 기본 법칙에 따라 간편화를 하는게 아닌 카노 맵을 사용해서 간편화를 해보자.
간편화를 진행할 부울 식은 이전의 식을 재활용한다.
$E = a’b + abc + bc$
위 식은 3개의 변수를 가진 부울 식이다.
식을 간편화하기 위해서는 먼저 카노 맵을 그려야 한다.
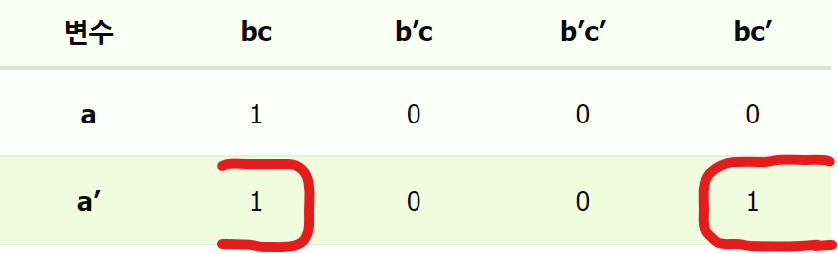
| 변수 | bc | b’c | b’c’ | bc’ |
|---|---|---|---|---|
| a | ? | ? | ? | ? |
| a’ | ? | ? | ? | ? |
위 카노 맵을 채워넣기 위해서 3번 표현 방법(3. 출력이 1인 기본 곱에 해당하는 민텀은 1로, 나머지는 0으로 표시한다.)을 사용한다.
1) 민텀을 찾아 1로 표기
minterm expansion 형태의 식에서 각 항으로부터 민텀을 찾아낸다.
- $a’b = a’b(c + c’) = a’bc + a’bc’$
- $abc$
- $bc = (a + a’)bc = abc + a’bc$
어차피 한 항만 1이어도 minterm expansion 형태에서는 전체 출력값이 1이 되므로, 찾아낸 민텀은 1로 표기하고 나머지는 0으로 표기하여 카노 맵을 채워넣는다.
귀찮으면 그냥 식 자체에 변수들의 값을 대입하여 출력값을 표기해도 된다.
(ex. 민텀 abc 는 a=1, b=1, c=1 로 사용해 출력값을 구해 카노 맵을 채워넣는다)
| 변수 | bc | b’c | b’c’ | bc’ |
|---|---|---|---|---|
| a | 1 | 0 | 0 | 0 |
| a’ | 1 | 0 | 0 | 1 |
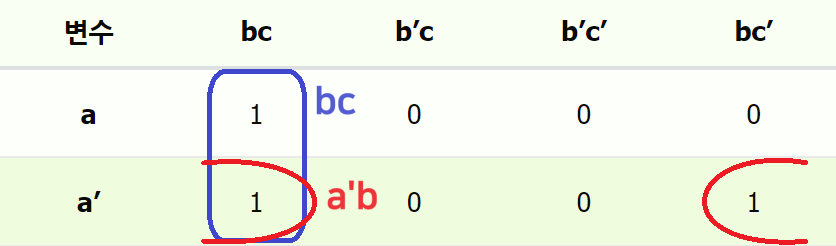
2) 값이 1인 인접 민텀끼리 묶기
이제 간편화를 위해 인접해있는 민텀들끼리 묶는다.
인접한 민텀을 찾을 때 주의사항!
표 형태로 표현했기 때문에 헷갈릴 수 있는데, 위 표에서 민텀 a’bc 와 a’bc’ 는 열이 끝과 끝으로 떨어져있어서 인접하지 않은 것처럼 보일 수 있다.
하지만 실제로는 두 최소항 사이에 단 하나의 변수(c)만이 변화했기 때문에, 이 최소항들도 인접해있는 것이다.
값이 1인 인접한 민텀끼리 묶으면 총 2묶음이 나온다.
각각의 묶음을 활용해 식을 다음과 같이 간편화가 가능하다.
- $abc + a’bc = (a + a’)bc =\;$$bc$
- $a’bc + a’bc’ = a’b(c + c’) =\;$$a’b$
- 간편화된 최종 식: $bc + a’b$
이러한 카노 맵을 활용한 간편화 방식은 식이 복잡해질 수록 대부분의 식들을 더 편하게 간편화 할 수 있다.
정리
데이터가 컴퓨터 내부에서는 실질적으로 게이트로 표현하고, 이 게이트는 부울대수를 통해 표현이 된다.
또 이러한 게이트들을 활용한 설계를 위해 진리표를 만들어서 설계도로서 활용한다.
이 진리표를 구현할 때, 개선 작업에 사용되는 부울 대수와 카노 맵에 대해서도 알아보았다.
이러한 내용들이 바로 조합회로의 근간이 되는 내용들이다.