컴퓨터 구조 - 2-5. 데이터의 표현(조합 논리회로, 기억회로, 순차회로)

게시 2024/05/15 업데이트 2024/06/04

By Hyechan Bang 25 분읽는 시간

이 포스트는 패스트캠퍼스의 “컴퓨터 공학 전공 필수 올인원 패키지 Online.” 강의를 보고 정리한 내용입니다.

앞서서

이전 포스트들의 내용을 종합해보면 먼저 이진법, 팔진법, 십육진법 등 여러가지 진법과 정수/실수의 표현법, 다양한 코드(디지털 코드, 에러 검출 코드)들을 포함한 표현법들이 있다.

다음으로는 이러한 이진 정보의 실제 표현이나 논리 연산들을 실제로 실행할 수 있도록 하는 하드웨어 개념인 논리게이트(스위칭 이론)와 복잡한 논리 연산식을 수리적으로 표현해 논리 회로의 형태를 기술할 수 있게하는 부울 대수의 개념과 법칙, 그리고 그런 부울 함수식을 간단화할 수 있는 카노 맵까지 정리했다.

조합 논리회로, 기억회로, 순차회로

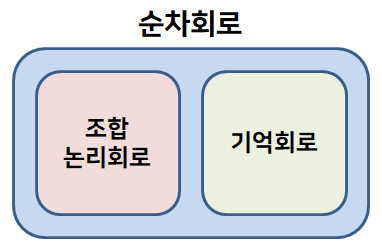
이러한 부울 함수식, 정확히는 특정 입력값으로 특정 출력값을 도출해낼 수 있는 논리 연산을 수행하는 하드웨어적인 내용이 바로 조합 논리회로이다. 이러한 조합 논리회로는 하나 또는 여러개의 게이트로 구성할 수 있다.

또한 조합 논리회로에서 연산된 출력값을 한번쓰고 버리는게 아니라 기억하기 위한 회로가 기억 회로이다.

그리고 위의 조합 논리회로와 기억회로들을 조합하여 구성해서 컴퓨터 구조를 구현하는 형태가 순차 회로이다.

이 회로들을 하나씩 더 자세히 살펴보자.

1. 조합논리 회로

조합논리 회로는 입력값과 출력값을 가진 논리 게이트의 집합으로, 입력값(0, 1)이 논리 게이트를 통해 출력값으로 나온다.

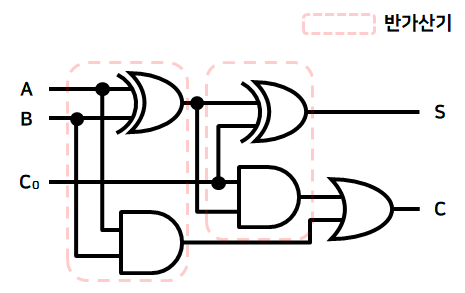
아주 기본적인 예로 이전 포스트의 반가산기(Half Adder)가 있다. 반가산기의 경우 출력값은 덧셈의 결과값 S 와 캐리비트 C 가 있다.

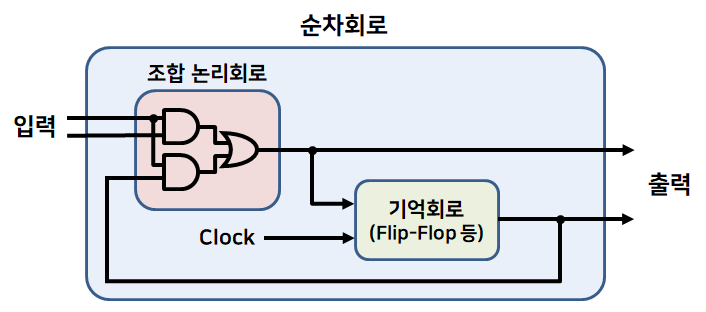
위 그림에서 조합 회로와 기억 회로가 같이 순차 회로로 구성된다.

1-1. 조합 회로 설계 절차

문제 제기 : 어떤 목적의 조합 회로를 만들고 싶다.
입/출력 기호화 : 입력/출력 변수에 문자 기호를 붙인다.(a, b, c, …)
진리표 유도 : 입력과 출력 사이의 관계를 진리표로 나타낸다.
간소화 : 출력에 대한 부울 함수식을 여러 방법을 통해 간소화한다.
논리도 작성 : 간소화된 식을 기반으로 게이트들을 사용한 논리도를 작성한다.

1-2. 대표적인 조합 회로

1) 가산기(Adder)

두 개 이상의 입력을 받아서 결과물을 출력하는 조합 논리회로이다.

대표적으로 반가산기(Half Adder)와 전가산기(Full Adder)가 있다.

반가산기는 이전 포스트의 내용을 참조하자.

반가산기에서 두 비트의 합 연산을 하나의 비트로 처리할 수 없어서 캐리 비트 C 를 추가했었다. 다만 반가산기에서는 발생한 캐리 비트를 처리하는 기능이 없고, 개선된 구조가 전가산기이다.

🔹전가산기

입력값에 이전 연산에서 발생한 캐리 비트 $C_0$ 가 추가되었고, 반가산기 구조 2개와 캐리 비트를 처리해주는 OR 게이트를 활용한다.

출력값의 부울 함수식은 다음과 같다.

$S = A\overline{BC_0} + \overline{AB}C_0 + ABC_0 + \overline{A}B\overline{C_0}$
$C = AC_0 + AB + BC_0$

2) 멀티플렉서(Multiplexer)

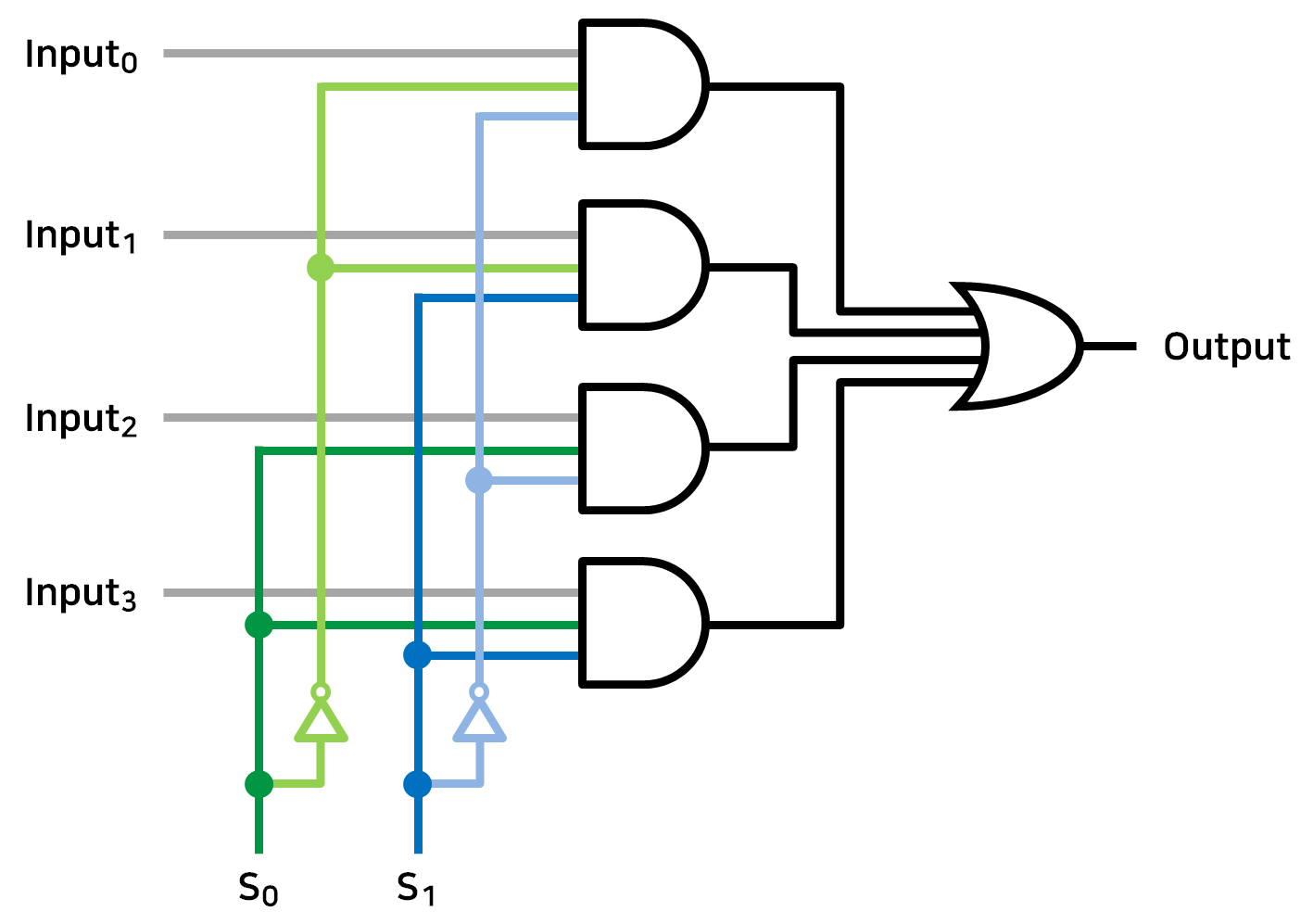
다수의 입력이 있을 때, 그 중 하나만을 신호 조작을 통해 선별적으로 출력하게 해주는 조합 논리회로이다.

4개의 입력값 $\mathbf{Input_0}$ ~ $\mathbf{Input_3}$ 을 받았을 때, 2개의 시그널 $S_0$, $S_1$ 을 활용해 입력값 중 하나의 값만 그대로 출력한다.

$S_0$	$S_1$	출력
0	0	$\mathbf{Input_0}$
0	1	$\mathbf{Input_1}$
1	0	$\mathbf{Input_2}$
1	1	$\mathbf{Input_3}$

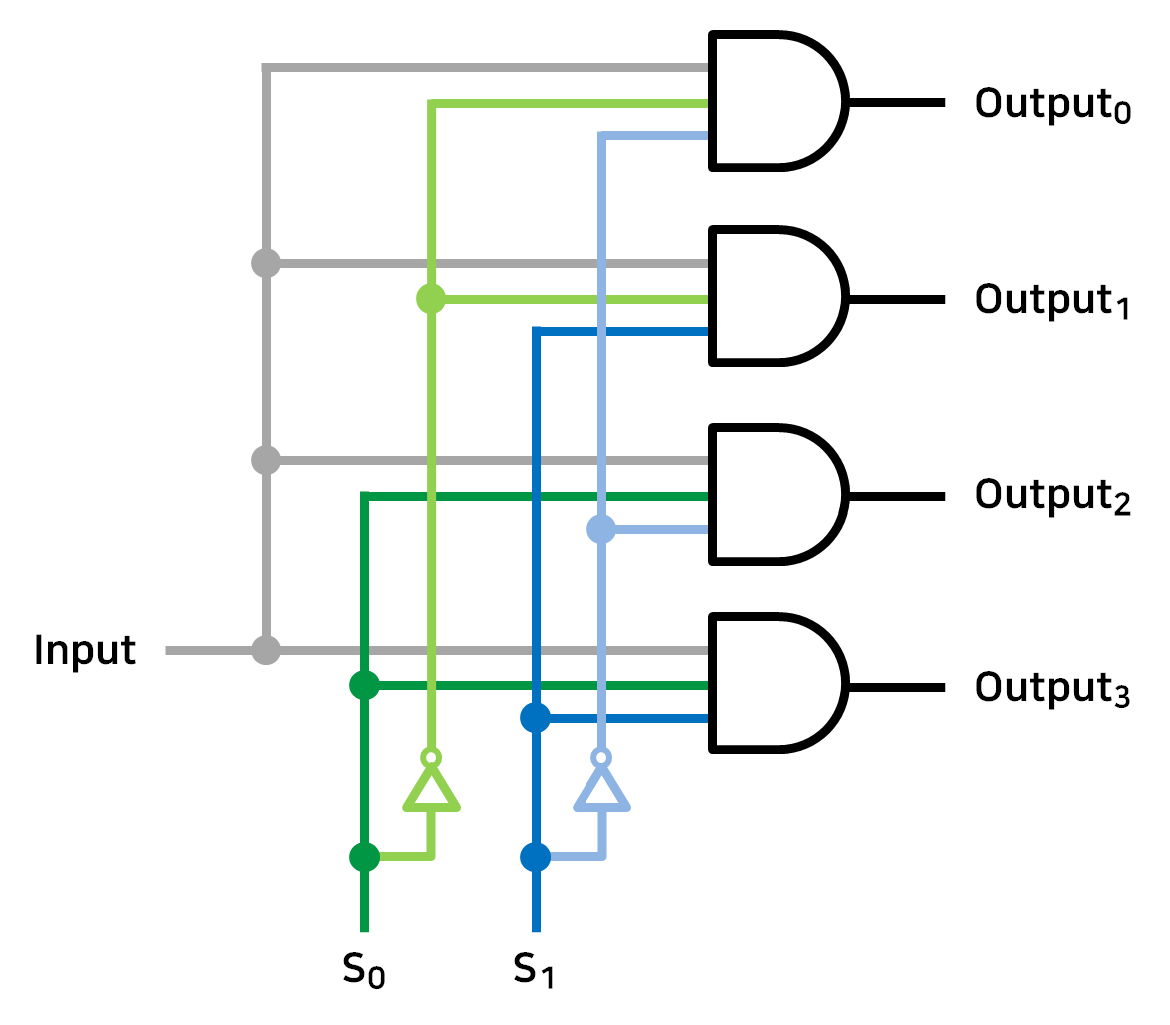
3) 디멀티플렉서(Demultiplexer)

멀티플렉서의 역 기능 개념으로, 하나의 입력값을 여러개의 출력으로 분해하는 기능을 가진 조합 논리회로이다.

위 그림을 예시로 들자면 시그널 $S_0$, $S_1$ 을 활용해 총 4가지의 출력핀 중 하나만 선택하여 입력값을 내보내는 논리 회로가 있다.

$S_0$	$S_1$	출력핀
0	0	$\mathbf{Output_0}$
0	1	$\mathbf{Output_1}$
1	0	$\mathbf{Output_2}$
1	1	$\mathbf{Output_3}$

2. 기억회로

디지털 시스템의 대부분이 조합 논리회로를 가지고 있으며 순차회로로 구현되는 저장요소를 필요로 한다. 이러한 저장요소 역할을 하는 기억소자의 대표적인 것이 플립플롭(Flip-Flop)이다.

2-1. 기억소자의 종류, 작동 원리

기억소자에도 대표적인 것이 Latch 와 Flip-Flop 이 있다. 하나씩 종류별로 알아보도록 하자.

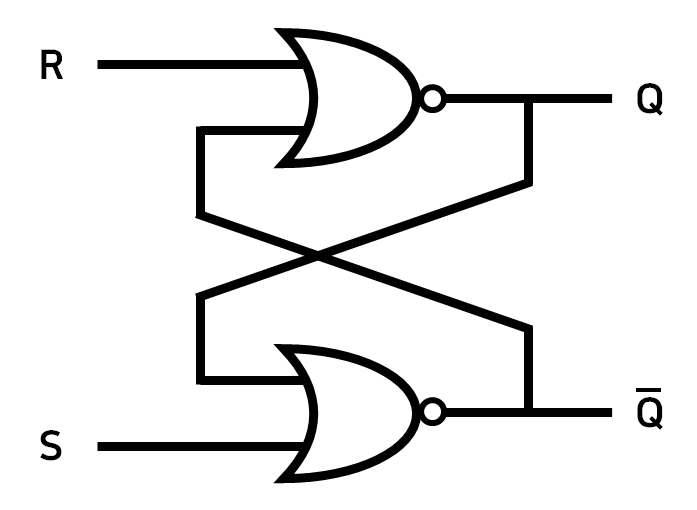
1) R-S Latch

1비트 값(0, 1)을 다음 제어 입력이 들어올 때까지 유지(기억)하는 기억소자이다.

이 Latch 는 NOR 게이트로 만들어진 Latch 이고, NAND 게이트로 만들어진 Latch 또한 존재한다.

먼저 Latch 의 입력값 R, S 에 따른 진리표를 살펴보자.

S	R	Q(T+1)	설명
0	0	$Q(T)$	No Change(상태 유지)
0	1	0	Reset
1	0	1	Set
1	1	-	Indeterminate(Forbidden; 부정)

먼저 기억할 것이 2가지가 있다.

NOR 게이트는 입력값이 하나라도 1인 경우 출력이 0이 된다.
$Q$ 값과 $\overline{Q}$ 값은 반대의 값을 가져야 한다.

따라서 R, S 값이 모두 1인 경우는 $Q$ 와 $\overline{Q}$ 값이 모두 0이 되므로 사용이 금지된다.

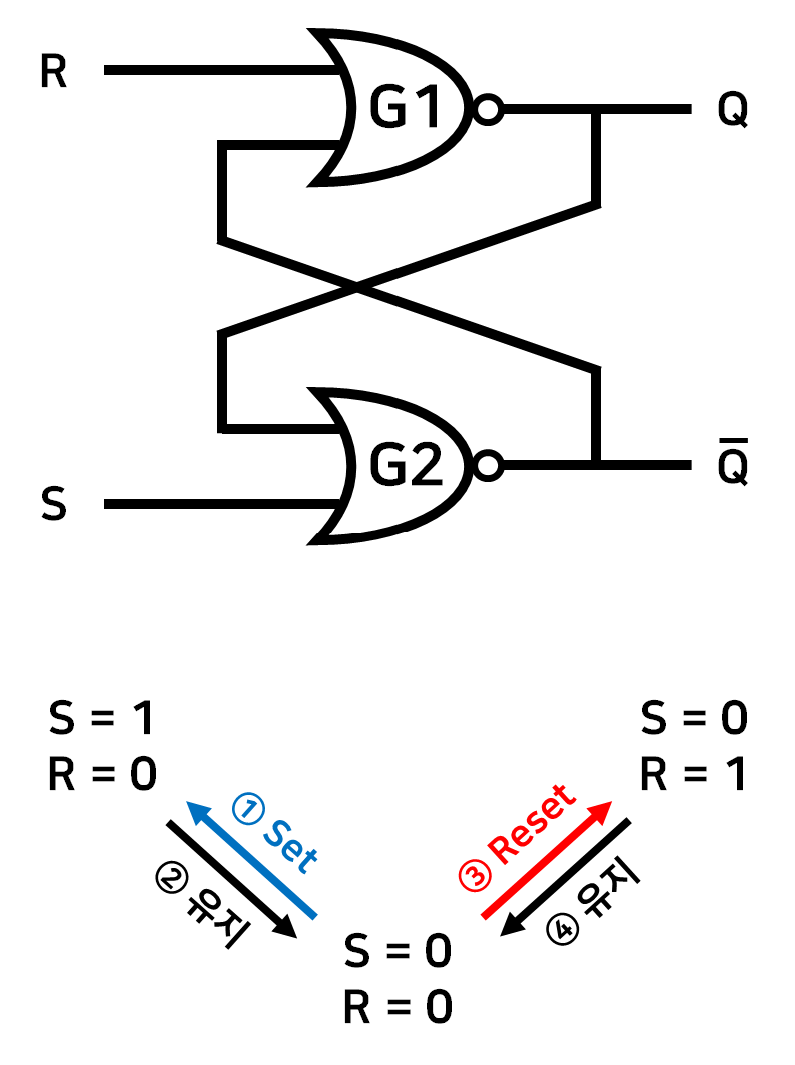
초기값은 모든 신호가 0인 상태를 가정하면 가장 먼저 NOR 게이트 G1 의 입력값은 0, 0 이 되므로 $Q = 1$ 이 되고(G1, G2 구조가 똑같고 동시에 켜지는데, 왜 G1 먼저 출력이 되는건지 궁금하긴 하다. 칩 내부 구조가 그렇게 되어있나? 아니면 어짜피 초기값은 안쓰니까 랜덤이어도 신경 쓸 필요가 없는걸까?), G2 의 입력값은 0, 1 이 되므로 $\overline{Q} = 0$ 이 된다.

따라서 입력값 $(R, S)$ 의 조작은 다음과 같다.

R-S Latch

$S = 1$ 로 세팅되면 G2 게이트의 출력은 $\overline{Q}(T+1) = 0$ 이 되고, $R = 0$ 이므로 반대쪽 G1 게이트는 입력값 0, 0 을 받아서 출력값은 $Q(T+1) = 1$ 이 된다.
다시 $S = 0$ 으로 세팅되면 G2 게이트의 입력값은 $Q(T) = 1$ 과 $S = 0$ 이 되므로 출력값은 $\overline{Q}(T+1) = 0$ 이 된다. 이 값과 $R = 0$ 값이 G1 게이트의 입력으로 들어가서 출력값은 여전히 $Q(T+1) = 1$ 로 유지된다.
$R = 1$ 로 세팅되면 G1 게이트의 출력은 $Q(T+1) = 0$ 이 되고, $S = 0$ 이므로 반대쪽 G2 게이트는 입력값 0, 0 을 받아서 출력값은 $\overline{Q}(T+1) = 1$ 이 된다.
다시 $R = 0$ 으로 세팅되면 G1 게이트의 입력값은 $\overline{Q}(T) = 1$ 과 $R = 0$ 이 되므로 출력값은 $Q(T+1) = 0$ 이 된다. 이 값과 $S = 0$ 값이 G2 게이트의 입력으로 들어가서 출력값은 여전히 $\overline{Q}(T+1) = 1$ 로 유지된다.

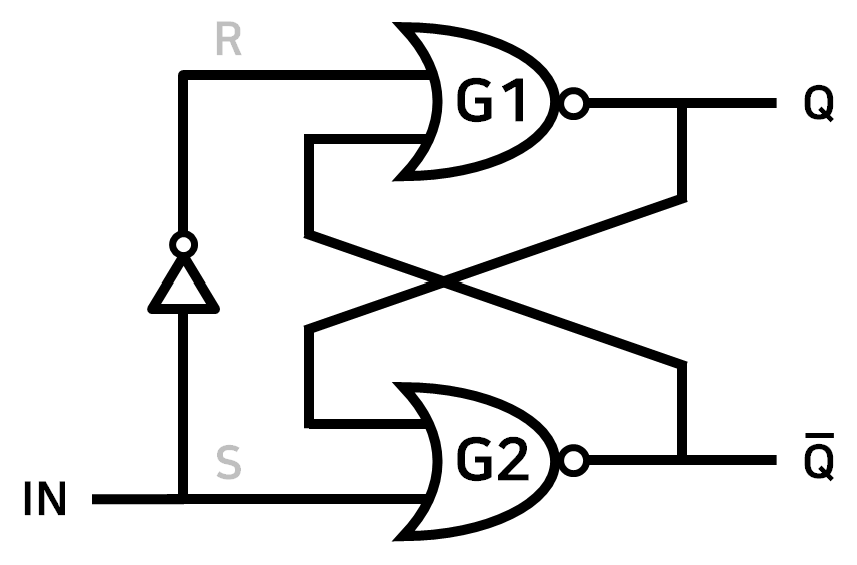
🔹R-S Latch with Single Input

R-S Latch 에서 두개의 입력값 R, S 를 하나로 사용할 수 있을까?

정답은 “할수는 있다” 이다. 아래의 그림을 보자.

보다시피 입력신호 IN 의 값을 하나는 반대로(NOT Gate; Inverter), 하나는 그대로 사용해 동시에 게이트 G1, G2 의 입력으로 보내고 있다.

입력신호를 하나로 만들긴 했으니 이에따른 진리표를 살펴보자.

$IN$	$R$	$S$	$Q$	$\overline{Q}$	설명
0	1	0	0	1	Reset
1	0	1	1	0	Set

보다시피 하나의 입력값으로 Set, Reset 을 모두 수행할 수 있다. 하지만!! 입력값을 하나로 만든것에따른 문제점도 존재한다.

기존의 R-S Latch 에서는 정확하게 입력신호에 3가지 state 가 존재했다. Single Input 에서도 가능한 Set, Reset 을 제외하면 나머지는 바로 No Change 즉, 값을 유지하는 state 이다.

따라서 입력값을 하나로 합쳤을 때의 문제점은 바로 Set, Reset 을 할 수는 있지만, 그러한 출력값을 유지할 수가 없다는 점이다.

이러한 문제점을 해결하기 위해서는, Set 과 Reset 을 할 때에만 IN 을 받아들이고 다른 때에는 무시하여 값을 유지하면 된다.

🔹R-S Latch with Enable

이제 문제점을 해결하기 위해 새로운 입력신호 EN(Enable) 를 사용해보자. 동작원리를 이해하기 위해 일단 입력신호 R, S 를 그대로 사용한다.

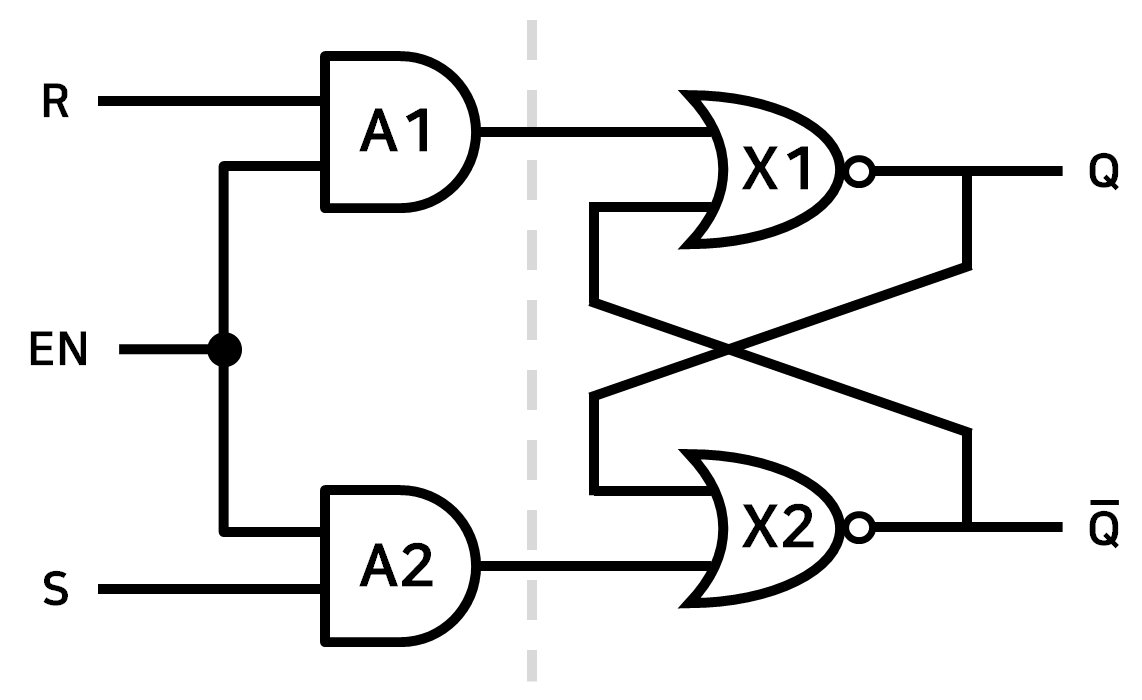
입력값 R, S 가 XOR 게이트와 바로 연결된 R-S Latch 에 Enable 신호가 추가된 형태의 Latch 이다.

Enable 의 값이 0인 경우 : R 값과 S 값에 상관없이 AND 게이트 A1, A2 가 모두 0 을 출력하기 때문에 기존의 R-S Latch 에서 $R = 0$, $S = 0$ 입력값을 받은것과 같이 출력값 $Q(T)$ 와 $\overline{Q}$ 를 유지하게 된다.

Enable 의 값이 1인 경우 : R 값과 S 값이 그대로 A1, A2 게이트로 출력되므로 R-S Latch 에서 처럼 출력값을 Set, Reset 할 수 있게된다.

즉 출력값을 변경하기 위해서는 EN 신호가 1 이어야 하며, EN 신호가 0 이면 다른 입력신호에 상관없이 출력값이 계속 유지된다.

어떻게 보면 EN 신호가 R-S Latch 자체를 켜고 끈다고 생각해도 될듯하다.

유튜브를 검색하다가 정말 설명을 잘해놓은 영상을 발견했다. 유튜버 Ben Eater 의 영상으로 구독자가 무려 122만명 ㄷㄷ;
R-S Latch : https://www.youtube.com/watch?v=KM0DdEaY5sY
R-S Latch with Enable, D latch : https://www.youtube.com/watch?v=peCh_859q7Q
다만 외국인 유튜버라 영어를 해야한다는 점~ 설명을 알아들을 수 있기만 한다면 최고의 영상인 것 같다. 뭐 못알아들어도 대충 눈치로.. 알 수 있잖아?

이제 입력신호 R, S 를 IN 하나로 통일한 경우를 봐야하는데, 이 구조가 바로 D Latch 더라. 자연스럽게 넘어가보자.

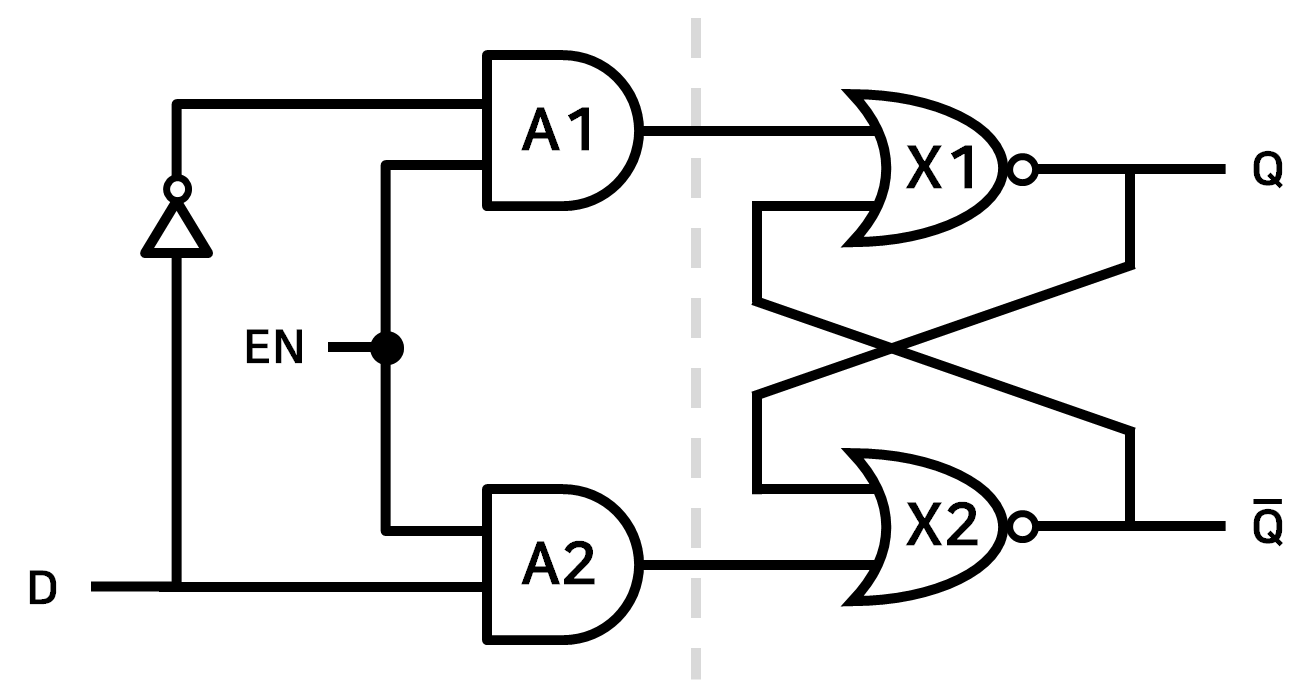
2) D Latch

입력신호를 D 하나로 통합시켰다. 이전의 R-S Latch with Single Input 에서 확인한대로 D 를 통해 출력값 Q 를 Set, Reset 할 수 있다.

이러한 출력값을 유지하기 위해서는 EN 을 1 로 설정한 상태에서 D 를 설정(Set: 1, Reset: 0)하고 원하는 출력값 Q 가 되었을 때 EN 을 0 으로 설정하면 유지가 가능하다.

다시말해 EN 이 1 일때 입력값 D 를 조작해 출력값 Q 를 설정할 수 있고, EN 이 0 이 되는 시점에서의 Q 값이 계속 유지된다는 뜻이다.

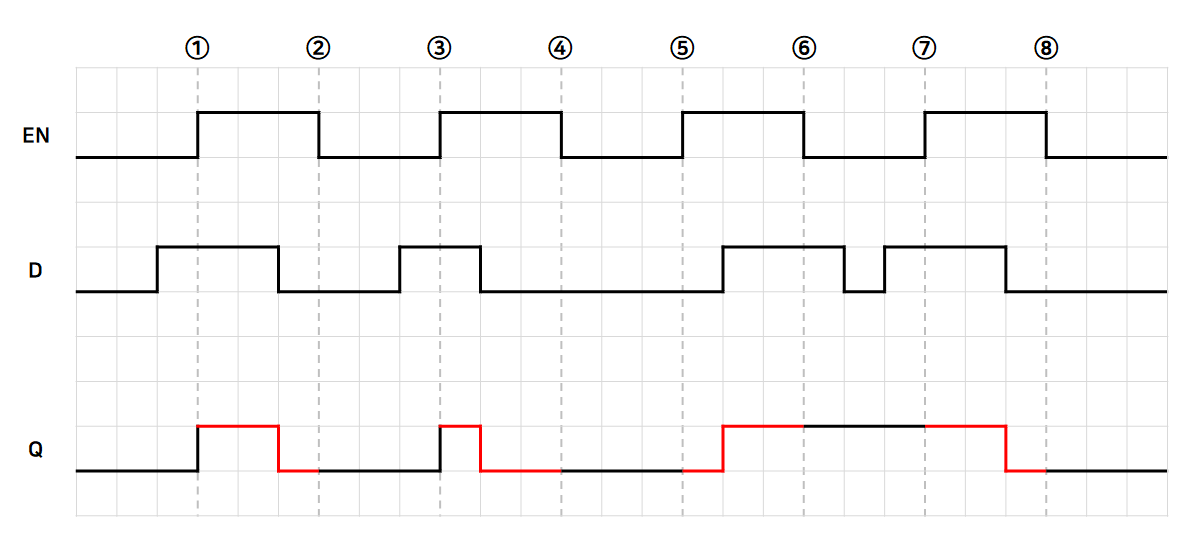
간단한 타이밍 다이어그램을 살펴보자.

출력값의 변화는 EN 신호가 켜진 후 꺼질때 까지만 보면 알 수 있다.(1~2, 3~4, 5~6, 7~8)

첫번째 EN 신호가 꺼지는 시점 ② 의 D 값은 0 이므로 출력값 Q 또한 0 이 되고, 이 값은 다음 EN 신호가 활성화되기 전까지 무조건 유지된다.

마찬가지로 다음 EN 신호가 켜지는 시점 ③ 에서는 D 의 값이 1 이므로, 출력값 Q 도 1 로 설정된다. 다시 EN 이 꺼지기 전 D가 0 으로 설정되므로 Q도 0으로 변하고, EN 신호가 종료되는 시점 ④ 의 값인 출력값 0 이 다음 EN 신호가 켜질때까지 유지된다.

이러한 원리를 이해하면 나머지 부분도 쉽게 이해할 수 있다. 그러나 대부분의 디지털 논리 회로에는 더욱 복잡하고 많은 양의 Latch 들이 각각 다른 값들을 출력한다.

이러한 관점에서 중요해지는 부분이 바로 회로의 다양한 소자들의 동기를 맞추는 것이다. 다음 소자로 넘어가보자.

3) D Flip-Flop

일반적으로 각 소자들의 동작들을 모두 동기화시켜주기 위해 클락이 존재한다.

또한 출력값의 설정을 EN 이 활성화된 시간 안에서 자유롭게 설정하는 것 보다는 짧은 Clock 신호가 잠깐 활성화된 특정 시점에 설정하는 것도 중요하다.

이러한 동작을 위해 만들어진 Latch 의 변형 형태가 Flip-Flop 이다.

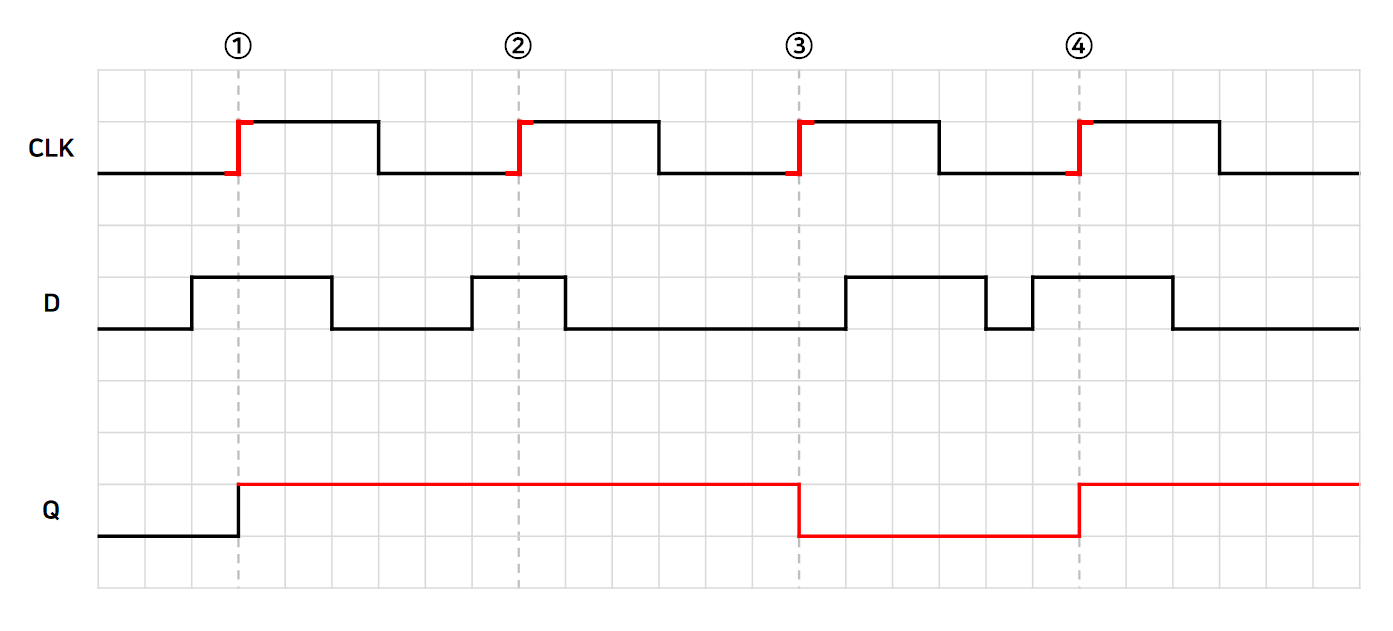
이번에도 타이밍 다이어그램을 살펴보자.

Latch 와 달라진 것은 출력값을 설정하는 시점이다.

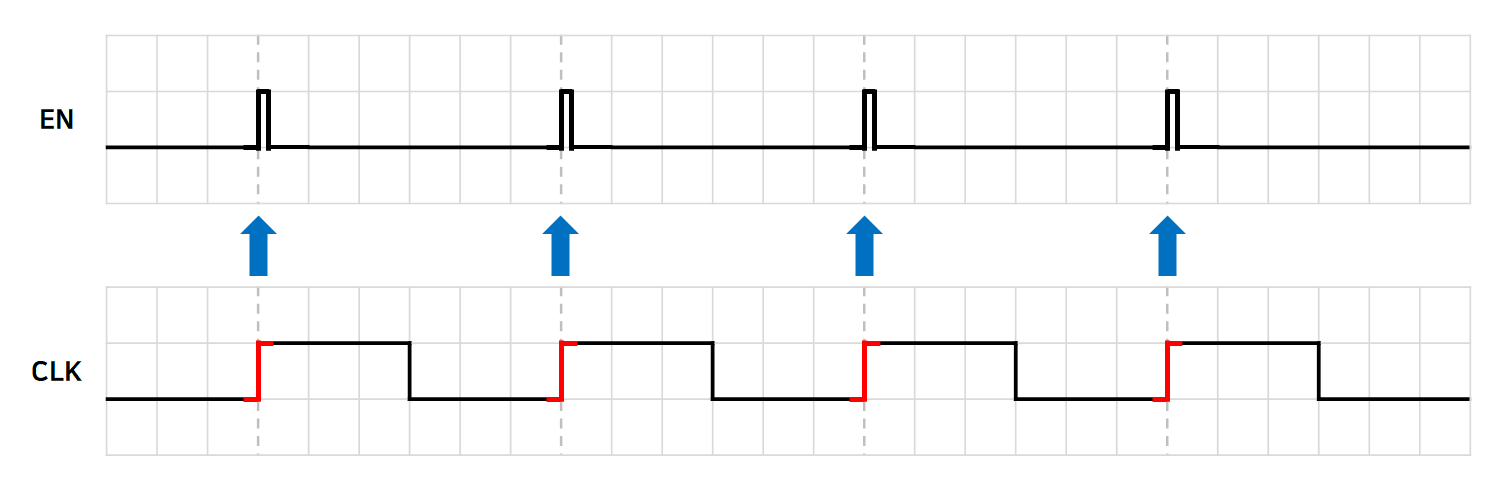
조금 더 자세히 말하자면 EN 신호의 긴 활성화 시간과는 다르게, CLK 이 활성화되는 그 짧은 시점(1, 2, 3, 4)에만 입력값 D 로 출력값 Q 를 설정할 수 있게 하자는 컨셉이다.

이러한 컨셉에 맞게 CLK 신호에 따른 EN 신호를 추가해 다시 그려보면 아래와 같은 뜻이 된다.

CLK 이 활성화 되는 시점을 감지해서 그 짧은 시점에만 입력값을 사용할 수 있게 EN 이 설정된다. 이러한 EN 신호를 만들어주는 회로를 Edge Detector 라고 한다. 그렇다면 이 Edge Detector 의 실제 회로 구성은 어떤것들이 있을까?

흠터레스팅….

그 방법은 바로바로…… 이 회로다!

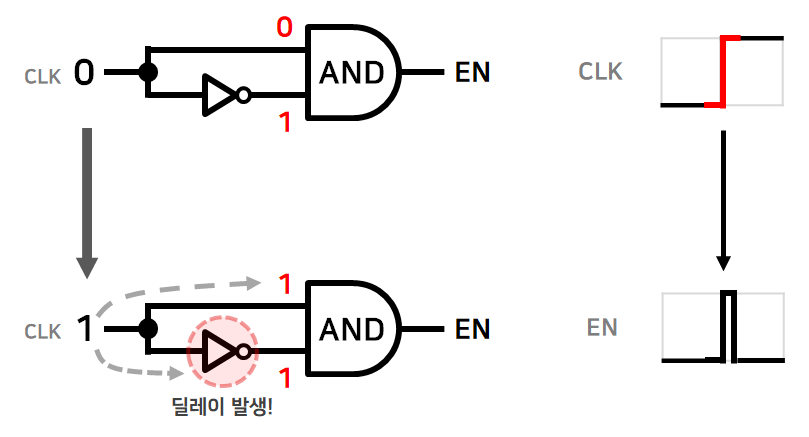
하나의 신호를 두개로 나누어 AND 게이트의 입력으로 사용하는데, 한 쪽에는 인버터를 통한 반대값을 입력시켜준다.

초기에는 입력 신호가 0 이고, AND 게이트에는 0 과 1 이 입력되기 때문에 EN 신호가 0 으로 유지된다.

다음으로 입력 신호가 1로 바뀐 시점인데, 인버터가 존재하지 않는 쪽은 바로 1 이 입력되지만, 인버터가 있는 쪽은 사실 몇 나노초(ns)의 딜레이가 실제로 존재한다.

이러한 사실로 인해 내부적으로는 CLK 신호가 1로 바뀌고 인버터를 통과하는 아주 짧은 시간동안 AND 게이트의 입력값이 1, 1 로 유지되고 EN 신호가 1로 설정된다.

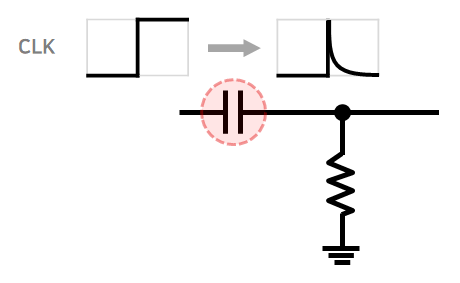
또 다른 방법으로는 저항과 캐패시터를 사용하는 방법인데, 이 방법은 AND 게이트처럼 칩을 사용하지 않기 때문에 더 쉬운 방식이다. 그림으로 살펴보자.

CLK 신호가 켜지고 캐패시터로 전기가 들어가면 캐패시터가 충전된다. 캐패시터가 충전될수록 통과하는 전류는 줄어든다. 캐패시터가 모두 충전되면 결국 전압는 0 이 된다.

신호가 줄어드는 속도는 캐패시터의 용량과 저항값을 곱한 값에 따라 결정된다.
(Ex. $0.1\mu F * 1K\Omega \; = \; 10^-7 * 10^3 \; = \; 0.1ms$)

그 외의 Flip-Flop

Flip-Flop 들은 다양한 종류가 있고, 그 쓰임새가 다 다르다.

D Flip-Flop 외에도 SR Flip-Flop, JK Flip-Flop, T Flip-Flop 등이 있다.

3. 순차회로

순차회로는 기억회로인 Flip-Flop 과 조합회로인 게이트를 서로 연결한 것이다. 순차회로의 외부 출력은 외부 입력과 Flip-Flop 의 현 상태의 함수로 표시된다.

3-1. 순차회로의 상태표, 상태도

순차회로는 입력, 출력 및 Flip-Flop 의 상태로부터 특성을 알 수 있다.

즉, 다음 상태와 출력은 현재 상태와 입력과의 함수 형태를 가지며 이 사이의 관계도를 상태표라고 한다.

이러한 상태표를 그림으로 도시하면 상태도가 된다.

상태표 예시

	Present			Next
State		Input	State		Output
A	B	X	A	B	Y
0	0	0	0	0	0
0	0	1	0	1	0
0	1	0	0	0	1
0	1	1	1	1	0
1	0	0	0	0	1
1	0	1	1	0	0
1	1	0	0	0	1
1	1	1	1	0	0

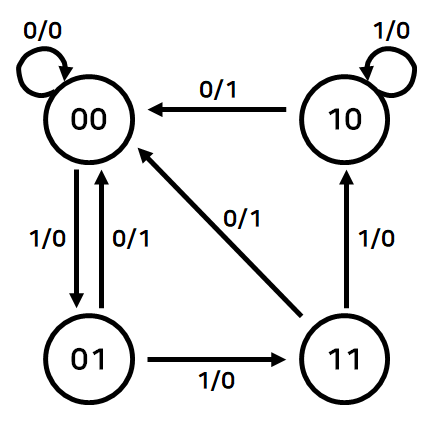
상태도 예시

이러한 정보들은 CPU 등 여러가지 상태값의 회로를 구성하고 만들 때 상태값에 대해 표현하는 방법들로, 뒤에서 더 자세하게 다루게 될 것이다.

정리

조합회로와 기억회로(Flip-Flop)이 결합이 됐을 때, 진정한 형태의 회로인 순차 회로가 된다.

다시말해 조합논리회로는 큰 회로를 구성하는 소단위의 완성된 회로라고 볼 수 있다.

조합논리회로의 결과값을 저장하기 위한 회로가 기억회로로, 동기화를 위해 Clock 기반으로 동작하는 Flip-Flop 과 조합논리회로가 연결되면 순차 회로가 된다.

CS, 컴퓨터구조

CS 컴퓨터구조