JAVA 알고리즘 복습 1
서론
이 포스트는 코딩 테스트를 위해 수강했던 패스트캠퍼스의 알고리즘 강의 한 번에 끝내는 코딩테스트 369 Java편 초격차 패키지 Online. 의 류호석 강사의 강의를 복습하며 정리한 내용입니다.
알고리즘이란?
문제를 해결하기 위한 절차(방법)이다.
주어진 문제에 맞춰서 입력을 넣으면 원하는 출력을 얻을 수 있도록 해주는 프로그래밍이다.
문제에 어떤 알고리즘을 사용하느냐에 따라 성능이 차이가 나기 때문에, 문제에 맞는 알고리즘을 사용해야 한다.
알고리즘에 좋은 습관은?
🔹문제를 올바른 순서로 이해하자
- 시간, 메모리 제한 확인하고 문제를 꼼꼼히 읽기
- 제공되는 정보들과 예제 데이터를 이해
- 가능한 최대, 최소 정답에 맞는 데이터를 직접 생성
🔹시간 복잡도, 공간 복잡도 계산
문제를 풀기전에 제한시간을 맞출 수 없는 알고리즘의 경우를 제외할 수 있다.
| 알고리즘 | 시간 복잡도 | 공간 복잡도 |
|---|---|---|
| BFS, DFS | O(V+E) | O(V+E) |
| Dijkstra | O(E log E), O(E log V) | O(V+E) |
| Quick Sort | 평균 O(N log N), 최대 O(N^2) | O(V) |
| Binary Search | O(N log N) | O(N) |
🔹코드를 함수화해서 효율적으로 구현
같은 코드의 반복은 함수화해서 효율적으로 구현한다.
🔹부분 점수를 챙긴다.
여러 문제의 부분점수를 챙기는 것이 한 문제만 다 푸는것보다 높은 점수를 챙기는 경우가 생긴다.
완전 탐색(Brute Force)
문제 해결을 위한 모든 경우의 수를 전부 탐색한다.
단순 for 문 만이 아닌 재귀를 통한 Back Tracking 상황도 해결할 줄 알아야 한다.
가장 기본적인 접근방식으로, 많은 연습이 필요하다.
부분점수를 얻기는 좋으나, 시간 복잡도가 높은 편이다.
완전 탐색의 종류
전체 N 개의 데이터에서 M 개를 고르는 문제의 경우
위 문제들의 시간복잡도와 공간복잡도를 계산해보면 다음과 같다.
| 중복 \ 순서 | 순서 있음 | 순서 없음 |
|---|---|---|
| 중복 허용 | 시간복잡도 : $O(N^M) = 7^7 \approx 82$만 공간복잡도 : $O(M)$ | 시간복잡도 : $O(N^M) = 8^8 \approx 1677$만 보다 작음 공간복잡도 : $O(M)$ |
| 중복 제외 | 시간복잡도 : $O({N \atop M}P) = O(\frac{N!}{(N-M)!})$ $= \frac{8!}{0!} = 40,320$ 공간복잡도 : $O(M)$ | 시간복잡도 : $O({N \atop M}C) = O(\frac{N!}{M!(N-M)!})$ $= \frac{8!}{4!4!} = 70$ 공간복잡도 : $O(M)$ |
응용 문제
BOJ 14888 - 연산자 끼워넣기, BOJ 9663 - N Queen., BOJ 1182 - 부분수열의 합
N Queen 에서의 팁
- 우상향, 우하향 대각선의 경우 행,열 좌표의 합과 차로 체크가능
- 반복문은 행, 열 두가지가 아니라 하나에 대해서만 돌리면 됨.(어짜피 행이나 열 1개 당 무조건 1개의 퀸이 들어가기 때문)
부분수열의 합 에서의 팁
- 전체 수열에서 각 요소를 사용/미사용 선택하는 문제이기 때문에, 전체 경우의 수는 $2^N$개 이다.
정렬 응용법(Sort Application)
정렬이란 주어진 특정 기준에 맞춰서 요소들을 나열하는 것을 뜻한다.
이러한 정렬 문제를 풀기 위해서는 몇가지 조건이 필요한데, 아래의 내용을 참조하자.
정렬 조건 설정
JAVA 에서는 정렬을 위한 기준을 Comparable<T> 인터페이스를 통해서 구현할 수 있다.
자세한 내용은 아래의 소스코드를 참조해보자.
1
2
3
4
5
6
7
8
static class Element implements Comparable<Element> {
public int value;
@Override
public int compareTo(Element other){
return value - other.value;
}
}
내부의 compareTo 메서드를 구현해야 하는데, 메서드에서 사용하는 매개변수는 현재 원소와 비교가 될 다른 원소이며, return 값이 음수이면 현재 원소가 우선, 양수이면 다른 원소가 우선, 0이면 동일한 기준값이라고 판단하여 정렬한다.
시간 복잡도
복잡하게 들어가지 않고, JAVA의 기본 정렬을 사용하는 입장에서는 N개의 원소를 정렬하기 위해 $O(N\log_2{N})$ 의 시간 복잡도를 갖는다고 알면 된다.(Ex. 10만개 원소 정렬은 160만 정도의 시간복잡도)
JAVA의 기본 정렬 Arrays.sort(arr) 에서 Primitive 원소와 Object 원소의 정렬에 차이점이 있는데, 아래 표를 참조하자.
| Primitive 원소 | Object 원소 |
|---|---|
Dual-Pivot Quick Sort(In-place Sort) | Tim Sort(Stable Sort) |
| 최소 $O(N)$ | 최소 $O(N)$ |
| 최대 $O(N^2)$ | 최대 $O(N\log_2{N})$ |
| 평균 $O(N\log_2{N})$ | 평균 $O(N\log_2{N})$ |
위에서 언급된 In-place, Stable 의 기준은 아래와 같다.
- In-place
- 원소의 개수가 N개 일 때, 정렬 과정에서 무시해도 될만큼의 메모리만 추가로 사용한다(Ex. 10만개의 원소 정렬에 10개정도 메모리만 더 추가로 사용한다.)
- Stable
- 정렬 기준으로 봤을 때 동등한 위상을 가진 원소들의 원래 순서 관계가 보존이 된다.
정렬의 특성
정렬을 적용한 후에 아래와 같은 특성을 가진다.
- 같은 정보들은 인접해있다.
- 각 원소에 가장 가까운 원소는 양 옆의 원소 중 하나이다.
예시 문제
응용 문제
BOJ 1015 - 수열 정렬, BOJ 11652 - 카드, BOJ 20291 - 파일 정리, BOJ 15970 - 화살표 그리기(이건 내 풀이가 좀 더 나은듯?)
탐색 - 이분 탐색(Binary Search)
수열에서 하는 탐색이란?
어떤 수열과 탐색값(혹은 범위)이 주어진다고 가정하자. 이 때 해당 탐색값이 존재하는지, 탐색범위안의 원소는 몇개인지, 탐색값과 가장 가까운 원소는 무엇인지 등을 찾는 행위이다.
여기서 만약 탐색대상인 수열이 정렬이 되어있는 상태 라면?
이분 탐색을 사용해 더 빠른 탐색이 가능하다!
이분 탐색이란?
정렬이 보장된 배열 에서, 탐색값 X 를 가지고 범위를 “이분” 하면서 탐색하는 방법이다.
단순히 값을 찾아내는 개념이 아니라, 찾아낸 값을 기준으로 조건을 만족하는 데이터가 얼마나 되는지(Ex. 찾은 값보다 큰 개수 등) 찾아내는 방법으로도 사용된다. 완전 탐색으로는 너무 오래 걸리는 경우 효율적으로 사용될 수 있다.
한번 이분할때마다 수열의 크기가 반씩 줄어들기 때문에 시간 복잡도는 $O(\log_2{N})$ 이다.
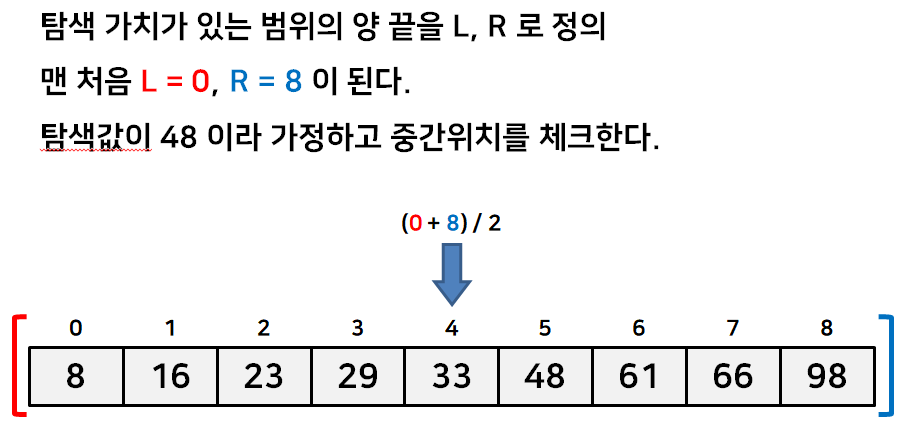
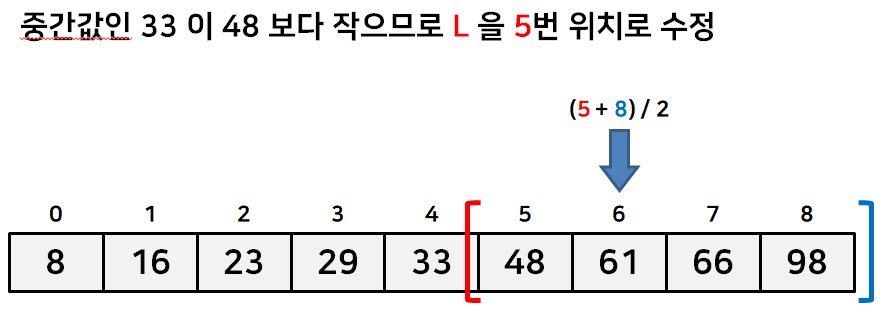
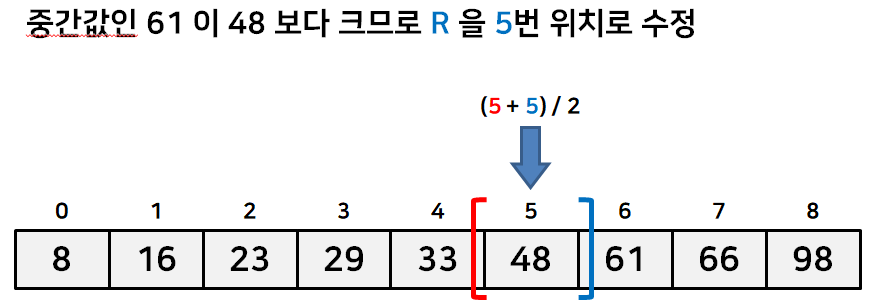
수열의 이분탐색의 간단한 예시를 아래 그림을 통해 살펴보자.
이런식으로 탐색 범위를 절반씩 좁혀나간다. 물론 위처럼 정확히 같은값을 찾는게 아니라 가장 가까운 값을 찾는 경우도 있다. 이런 경우는 L 이 R 보다 더 커지는 경우에 탐색을 종료하는 식으로 짜면 된다.
이러한 이분탐색의 사용이 익숙해지게 되면, 정렬을 깜빡하고 탐색을 시작하는 경우가 생기니 조심하자.
이분탐색은 정형화된 코드를 많이 사용하므로, 본인이 직접 짜보고 익히는게 중요하다.
예시 문제
BOJ 7795 - 먹을 것인가 먹힐 것인가, BOJ 2470 - 두 용액, BOJ 2470 - 두 용액
연습 문제
BOJ 1920 - 수 찾기, BOJ 1764 - 듣보잡, BOJ 3273 - 두 수의 합, BOJ 10816 - 숫자 카드 2
매개변수 탐색(Parametric Search)
이분탐색의 아이디어를 참조한 알고리즘이다.
예를들어, 0과 1로만 구성된 길이 1000개의 오름차순 배열이 있다고 가정했을 때, 0 과 1 의 경계가 어디인지 찾는 경우가 있다.
이 경우, 0 과 1 을 구분하는 작업에 걸리는 시간이 $T$ 라고 가정하면, 시간 복잡도는 $T\log_2{N}$ 이 된다.
이러한 매개변수 탐색의 핵심은 다음과 같다.
- 정답을 매개변수화 하고 Yes/No 문제로 바꿔서 보기
- 모든 값에 대해 Yes/No 를 채웠을 때, 정렬된 상태인지 보기(Yes 쭉 가다가 No 쭉 나와야 함. Yes / No 가 중간중간 섞이면 안됨)
- Yes/No 결정하는 문제를 풀기
위에 언급한 대로 Yes, No 가 정렬되기 않은 문제인제 이분 탐색을 하는 실수가 많이 나온다.
키워드
이러한 문제들의 공통적인 키워드는 ~ 의 최대값을 구하시오, ~ 의 최소값을 구하시오 가 자주 등장하며, 이런 키워드를 보면 매개변수 탐색을 시도해볼 가치가 있다.
연습문제
- BOJ 2805 - 나무 자르기, BOJ 1654 - 랜선 자르기, BOJ 2512 - 예산
- BOJ 2110 - 공유기 설치, BOJ 2343 - 기타 레슨, BOJ 6236 - 용돈 관리, BOJ 13702 - 이상한 술집, BOJ 17266 - 어두운 굴다리
- 고난이도 : BOJ 1300 - K 번째 수, BOJ 1637 - 날카로운 눈
투 포인터(Two Pointers)
문제를 풀 때 정답을 찾기위해 불필요한 부분들을 제외하는 것은 효율적으로 볼 때 필수적인 과정이다.
예를들어 위의 탐색 알고리즘에 사용한 기준점 L, R은 탐색범위를 반씩 좁혀가면서 불필요한 부분을 전체의 반씩 제외하는 과정을 거친다.
투 포인터 에서는 이 기준점 두 개에 의미를 부여해서 탐색 범위를 압축한다.
예를들면 아래와 같은 경우들이 있다.
1차원 배열에서 2개의 포인터를 만드는 경우
- 2개의 포인터가 모두 왼쪽에서 시작해 같은 방향으로 이동 하는 경우.
- 2개의 포인터가 양쪽 끝에서 시작해 서로를 향해 이동 하는 경우
문제에서 배열이라고 나오진 않지만 관찰을 통해 문제의 변수 2개의 값을 두 포인터로 표현하는 경우
키워드
이러한 투 포인터 알고리즘도 공통적으로 등장하는 키워드가 있다.
- 1차원 배열에서의 “연속 부분 수열” / “순서를 지키며 차례대로”
- 곱의 최소(Ex. A, B 의 곱의 최소를 찾을 때, A 가 커지면 B 가 작아져야 한다.)
위와 같은 키워드가 등장하면 투 포인터 접근을 해볼만한 가치가 있다.
연습 문제
- BOJ 1806 - 부분합, BOJ 2003 - 수들의 합2, BOJ 2559 - 수열, BOJ 15565 - 귀여운 라이언, BOJ 11728 - 배열 합치기, BOJ 2230 - 수 고르기
- BOJ 2470 - 두 용액, BOJ 3273 - 두 수의 합