JAVA 알고리즘 복습 2

서론

이 포스트는 코딩 테스트를 위해 수강했던 패스트캠퍼스의 알고리즘 강의 한 번에 끝내는 코딩테스트 369 Java편 초격차 패키지 Online. 의 류호석 강사의 강의를 복습하며 정리한 내용입니다.

---

알고리즘 분류

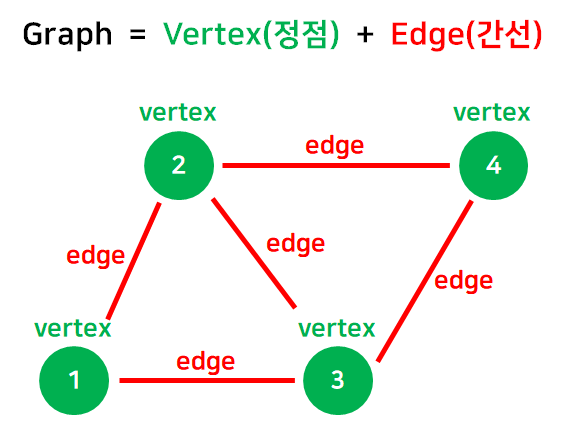
그래프(Graph)

자료구조에서 그래프란?

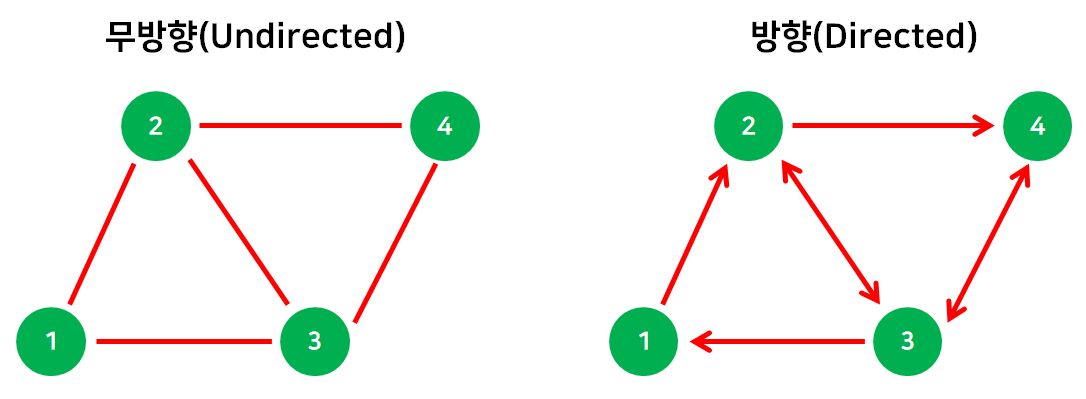
정점들을 잇는 간선의 종류는 2가지가 있다.

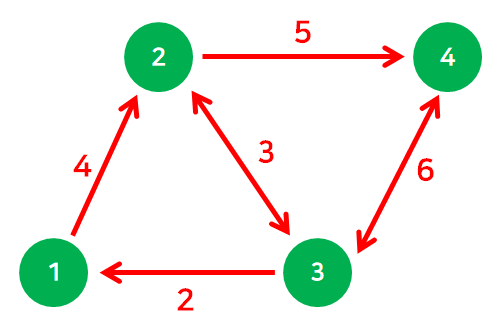
각 간선에는 가중치(Weight) 가 존재할 수 있다.

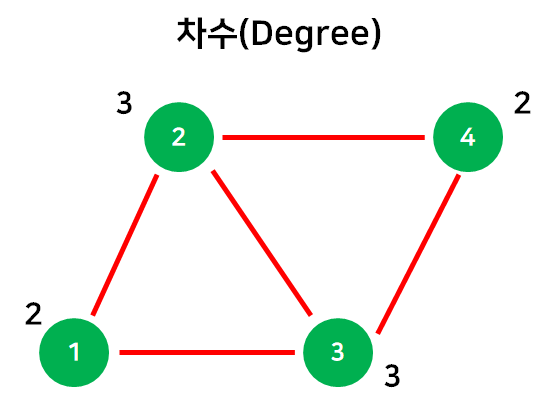
차수(Degree) 는 정점에 연결된 간선의 수를 뜻한다.

---

저장 방법

그렇다면 그래프는 컴퓨터에서 어떤 형태로 저장해서 사용할까?

대표적으로 두 가지 방법이 있다.

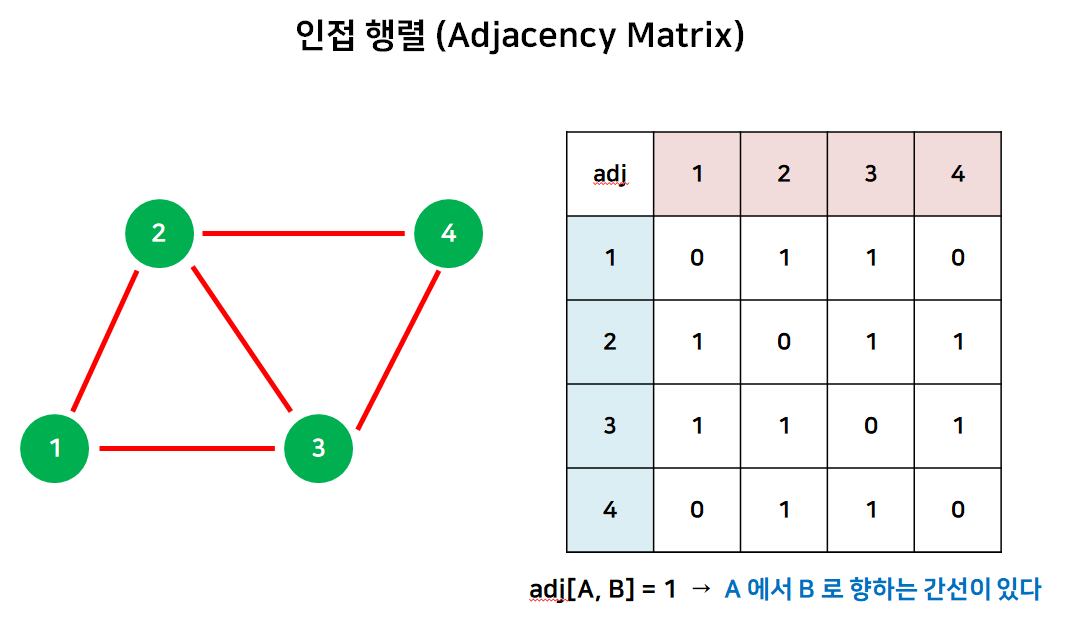
1. 인접 행렬(Adjacency Matrix)

• int[][] adj = int new[V][V]; 형태로 구현한다.
• 인접행렬을 만드는데 $O(V^2)$ 만큼의 공간이 필요하다. 이는 정점이 많아질수록 어마어마한 공간을 필요로 한다는 뜻이다.
• 모든 간선의 방향과 가중치가 행렬에 있기 때문에, 이동 가능 여부와 가중치 파악에는 $O(1)$ 의 시간복잡도를 가진다.
• 한 정점에서 갈 수 있는 정점들을 알기 위해서는 해당 행을 모두 봐야 하기 때문에 $O(V)$ 의 시간복잡도를 가진다.

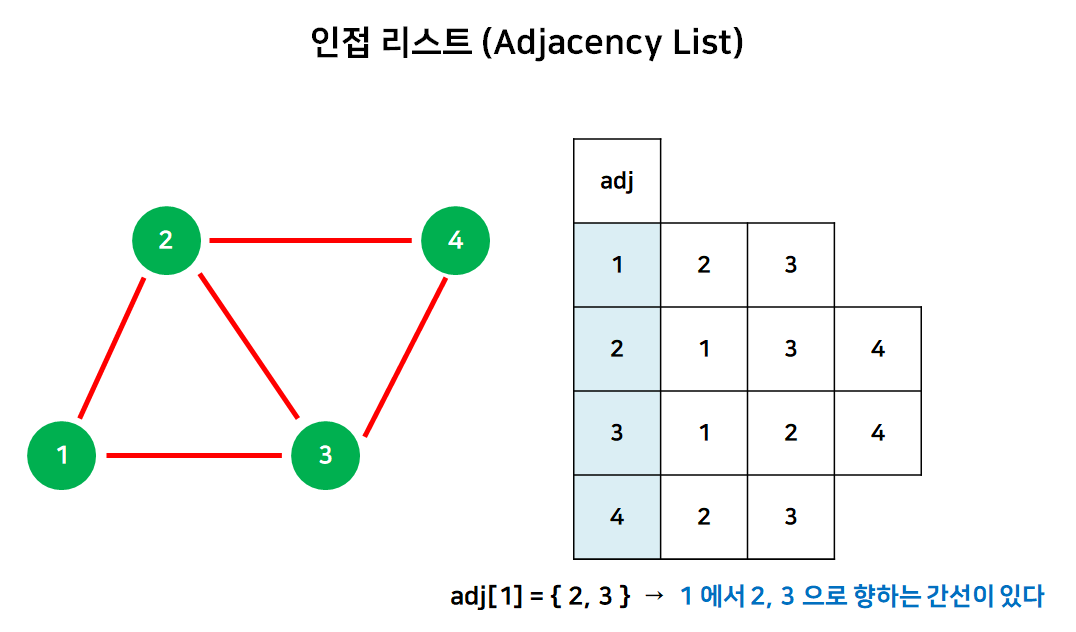
2. 인접 리스트(Adjacency List)

• ArrayList<Integer>[] adj; 형태로 구현한다.
• $O(E)$ 만큼의 공간이 필요하다.(차수 만큼의 공간이 필요하며, 이는 2E 이나 상수항은 생략) 이는 인접 행렬에 비해 훨씬 효율적이다.
• 이동 가능 여부와 가중치 파악에는 무방향이 $O(min(deg(A), deg(B)))$, 방향이 $O(deg(A))$ 의 시간복잡도를 가진다.
• 한 정점 A 에서 갈 수 있는 정점들을 알기 위해서는 $O(deg(A))$ 시간복잡도를 가진다.

---

탐색

한 시작점에서 간선을 자유롭게 사용해서 갈 수 있는 정점들은 무엇일까?

이를 찾는데는 2가지 방식이 있다.

1. 깊이 우선 탐색(DFS: Depth First Search)

아래와 같은 코드 형태를 가진다.

// x 로 갈 수 있는 걸 알고 방문한 상태
static void dfs(int x){
    // x 위치 visit 표시
    visit[x] = true;

    // x 에서 갈 수 있는 모든 곳 방문
    for(int y : x에서갈수있는점들){
        // 이미 방문한 경우 생략
        if(visit[y]) continue;

        // 같은 작업을 y에서도 실행
        dfs(y);
    }
}

main(){
    dfs(5);
}

위처럼 코드를 작성한 경우, dfs의 시간 복잡도는 내부의 for문을 보면 알 수 있다.

• 인접 행렬의 경우, $O(V^2)$
• 인접 리스트의 경우, $O(deg(1) + deg(2) + … + deg(V)) = O(E)$

2. 너비 우선 탐색(BFS: Breadth First Search)

큐(Queue) 자료구조를 활용하며, 아래와 같은 코드 형태를 가진다.

// 시작점 start 부터 갈 수 있는 정점들 모두 탐색
static void bfs(int start){
    Queue<Integer> queue = new LinkedList<>();

    // 맨 처음 방문할 start 부터 queue 에 넣는다.
    queue.add(start);
    visit[start] = true;

    while(!queue.isEmpty()){ // 확인할 점이 없을 때 까지 탐색
        int x = que.poll();

        for(int y : x에서갈수있는점들){
            // 이미 방문한 경우 생략
            if(visit[y]) continue;

            // 갈 수 있으면 queue 에 추가 후 visit 표시
            queue.add(y);
            visit[y] = true;
        }
    }
}

위처럼 코드를 작성한 경우, bfs의 시간 복잡도는 아래와 같다.

• 인접 행렬의 경우, $O(V^2)$ : int x = que.poll(); 에서 V 만큼, for(int y : x에서갈수있는점들){ 에서 V 만큼 반복
• 인접 리스트의 경우, $O(deg(1) + deg(2) + … + deg(V)) = O(E)$

주의할점은 꼭 visit 체크를 하는 올바른 시점은 queue 에 add 되는 시점이라는 것이다.

---

예시 문제

• BOJ 1260 - DFS와 BFS

응용 문제

격자형 그래프 연습

• BOJ 2667 - 단지번호 붙이기, BOJ 1012 - 유기농배추, BOJ 11724 - 연결 요소의 개수, BOJ 4963 - 섬의 개수, BOJ 3184 - 양
• BOJ 14502 - 연구소*

일반 그래프 연습

• BOJ 2606 - 바이러스, BOJ 11403 - 경로 찾기, BOJ 11725 - 트리의 부모 찾기
• BOJ 2251 - 물통*(물통 A, B, C 의 물 상태를 정점 하나로 본다. 강사의 풀이에선 State 라는 클래스를 만들어서 물통의 state 와 물을 옮기는 메서드를 만들어서 Queue 에 클래스를 넣고 bfs 를 돌렸다.)

---

BFS 탐색 + 최소 이동 횟수

시작 정점 A 에서 목표 정점 B 까지 가야 할 때, 필요한 간선 개수의 최소값(최소 이동 횟수)이 곧 최단거리가 된다.

단, 간선의 가중치가 존재하는 경우에는 해당되지 않는다.

키워드

이런 방식을 활용하는 문제에서 자주 등장하는 키워드는 “최소 이동 횟수”, “최단 시간” 등이 있다.

예시 문제

• BOJ 2178 - 미로 탐색, BOJ 7562 - 나이트의 이동, BOJ 2644 - 촌수 계산, BOJ 18404 - 현명한 나이트
• BOJ 1697 - 숨바꼭질, BOJ 1389 - 케빈 베이컨의 6단계 법칙, BOJ 5567 - 결혼식
• BOJ 3055 - 탈출, BOJ 7569 - 토마토, BOJ 2644 - 촌수 계산

---

트리(Tree)

트리(Tree) 구조는 그래프(Graph) 구조의 특수한 형태로, 그래프의 부분집합이라고 볼 수 있다.

트리의 특성

트리 구조는 그래프와 같이 정점과 간선으로 이루어져 있다는 것 외에도 아래와 같은 특성을 가지고 있다.

1. 어떤 정점이든 두 정점간 간선을 통해 이동이 가능하다.
   • (정점들이 모두 연결되어 있다.)
2. 사이클이 존재하지 않는다.
   • (간선들을 한번씩 사용하여 이동할 때 원래의 정점으로 돌아올 수 없어야 한다.)
3. 정점의 개수(V) 가 간선의 개수(E) 보다 1개 많다.

위 특성중 2개 이상을 만족해야 한다고 하는데, 그럼 2개만 만족하는 경우는 어떤건지 궁금하다.

---

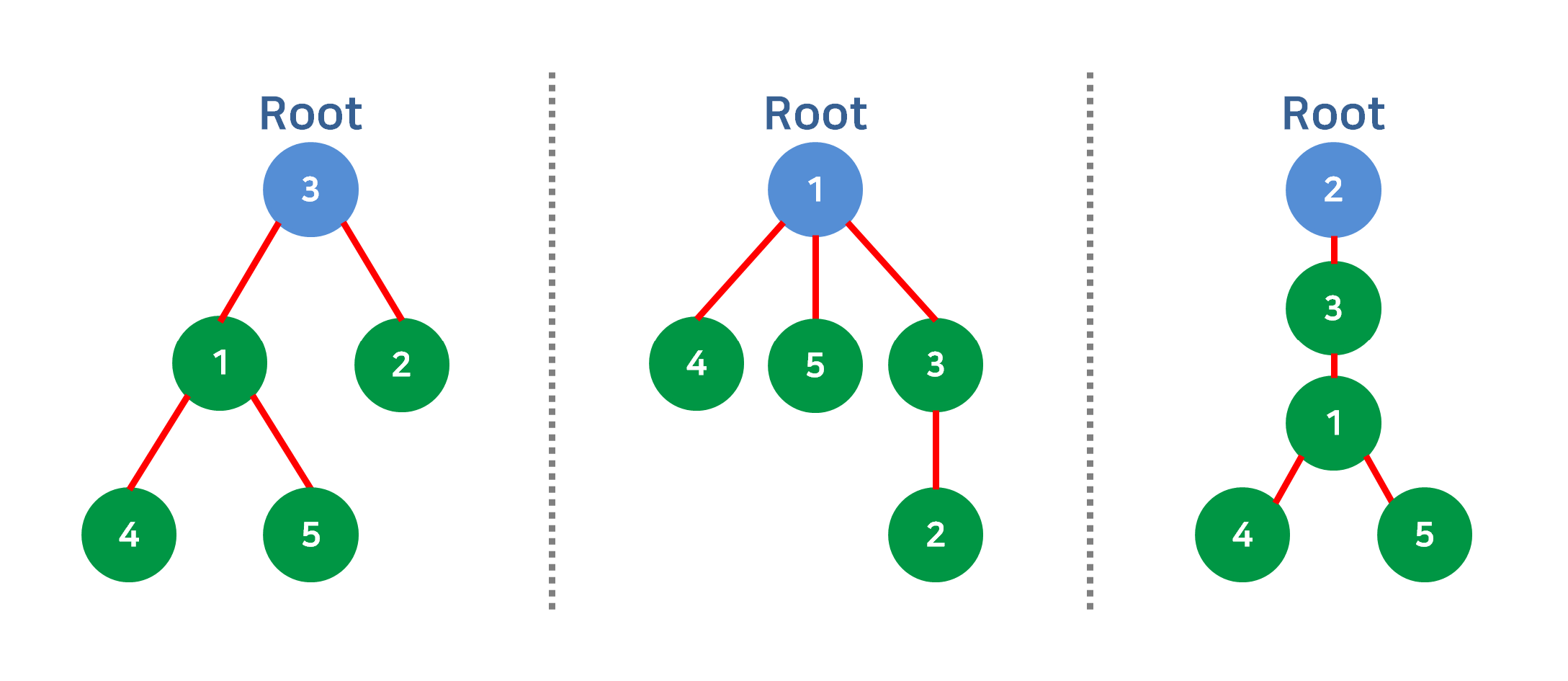
Rooted Tree

알고리즘에서 주로 사용되는 트리 구조이다. 이 구조에서 사용하는 용어들이 몇가지 있다.

1. Node : 그래프 구조의 Vertex 와 마찬가지로 트리를 구성하는 각 정점들을 뜻한다.
2. Root : 단어의 뜻 그대로 뿌리 노드, 즉 트리의 최상위 노드를 뜻한다. 다만 이 노드는 같은 그래프 구조라도 문제에서 주어지는 기준에 따라서 달라지는 부분이라고 봐야 할 것 같다.
   
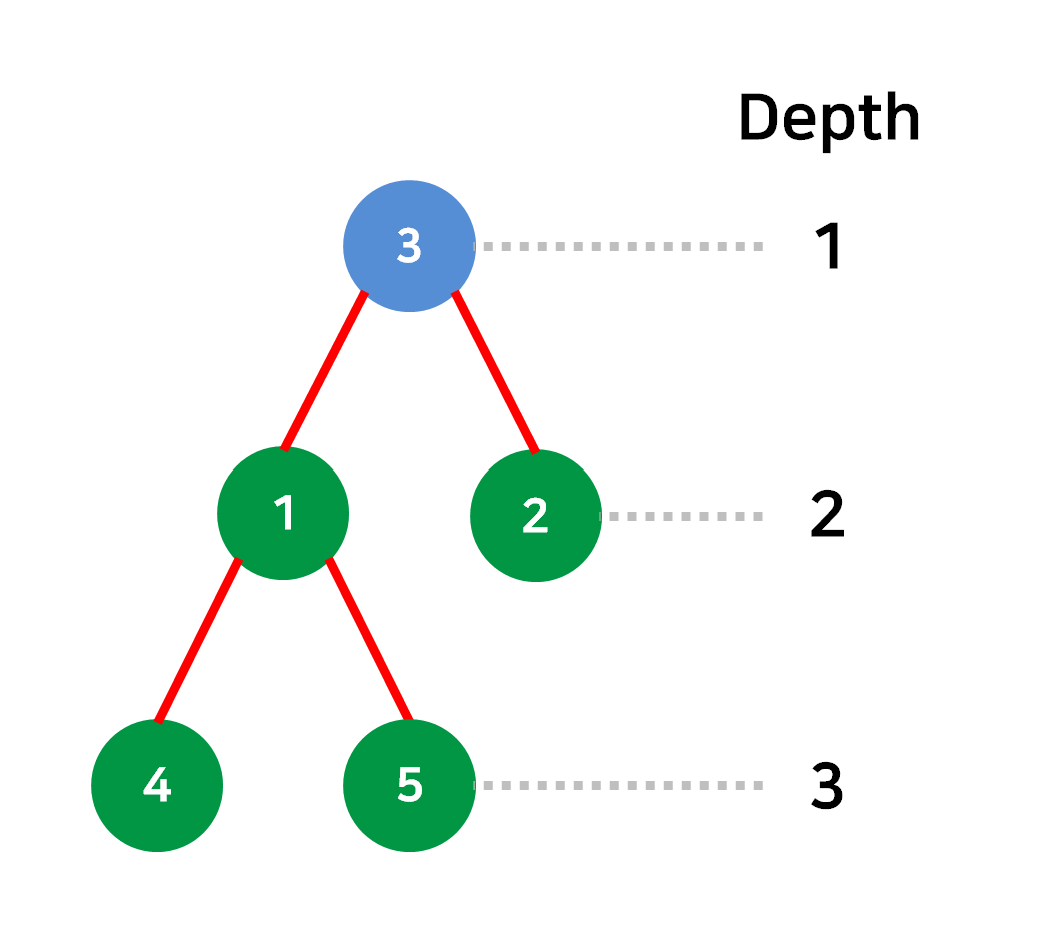
3. Depth : Root 노드로부터의 거리를 나타내기 위한 상대적인 깊이 개념이다. 보통 Root 노드의 Depth 를 0 또는 1 로 설정하고, 다음 노드부터 1 씩 늘어난다.
   
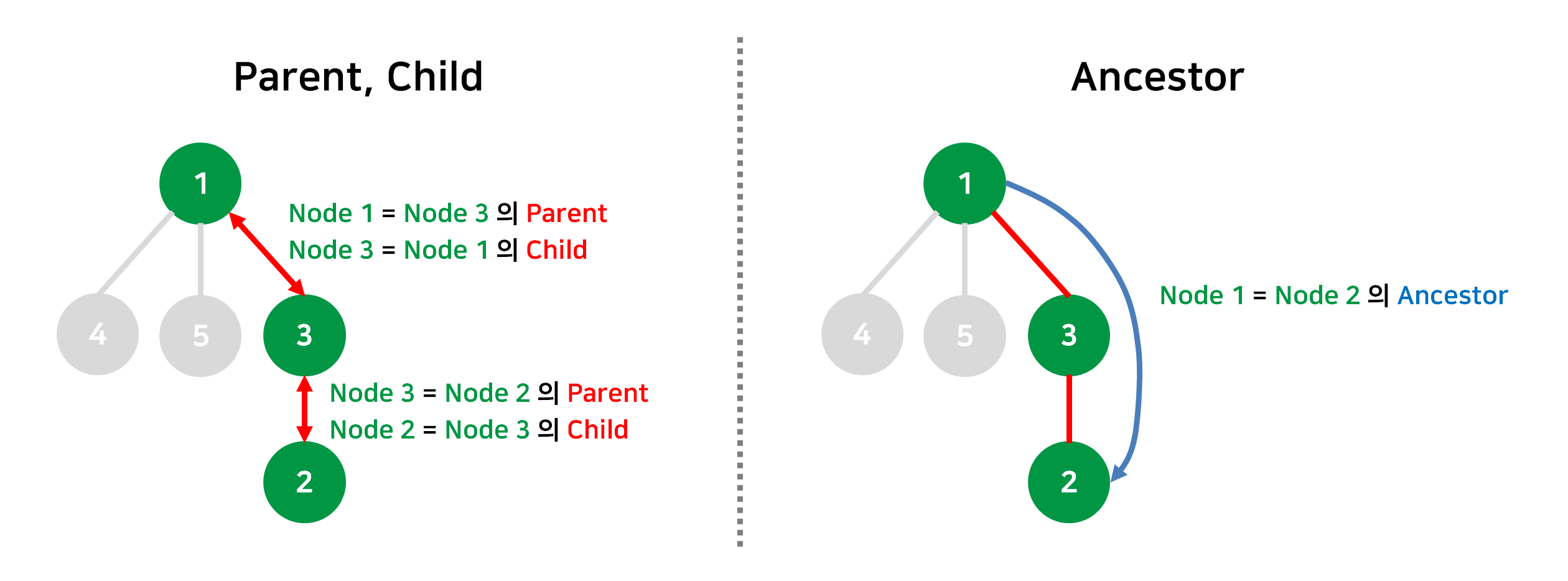
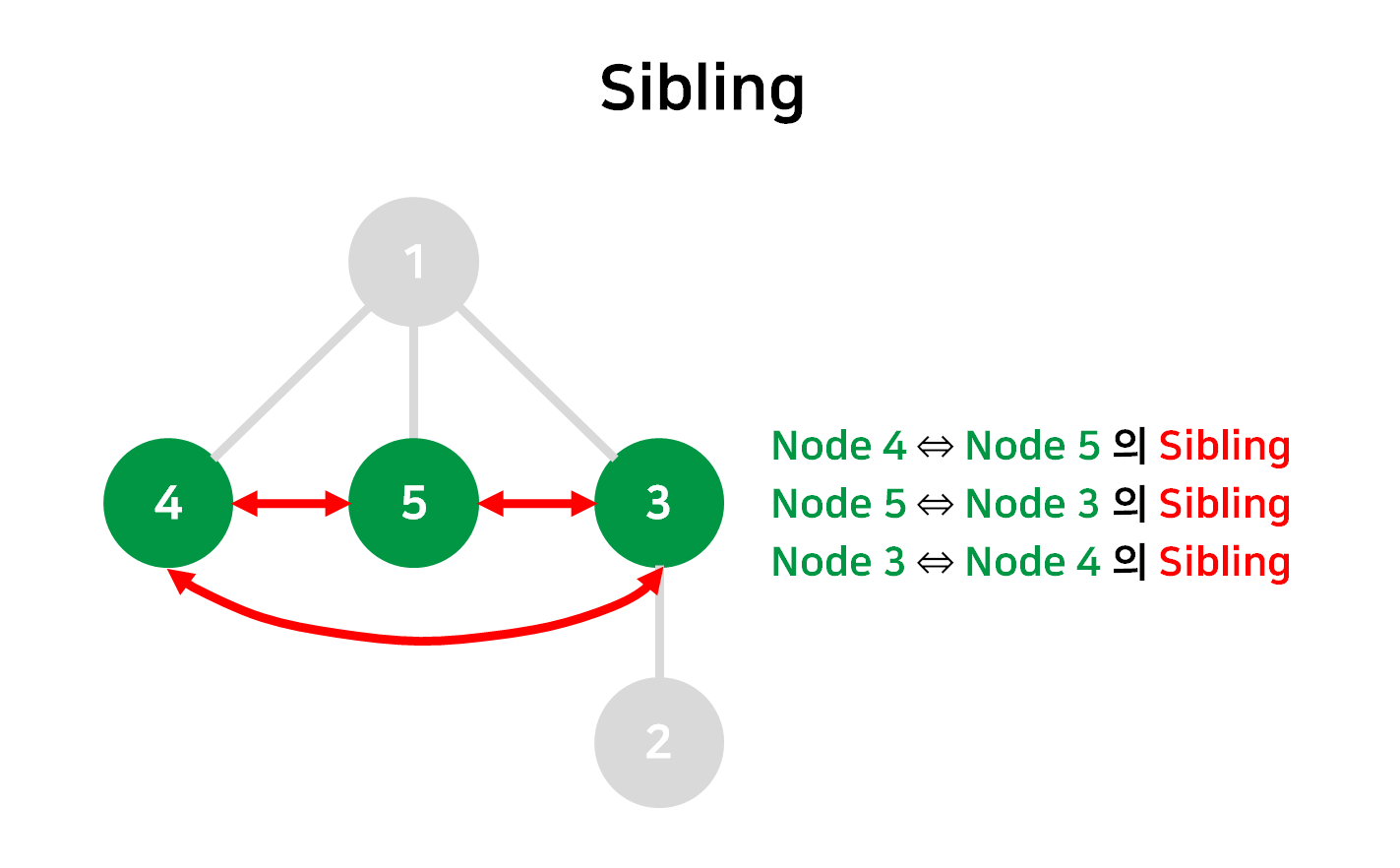
4. Parent, Child, Ancestor, Sibling
   • Parent 와 Child 는 간선 하나로 연결된 정점간의 부모 자식 관계를 나타낸다. Depth 가 작은 상위 노드가 Parent, 하위 노드가 Child 가 된다.
   • 한 Node 의 Ancestor 란 Parent, Parent 의 Parent, … 조상이 되는 모든 Node 를 뜻한다.(종종 자기자신도 포함되는 문제가 있다.)
     
   • Sibling 이란 같은 Parent 를 갖는 모든 Node 들을 뜻한다.
     
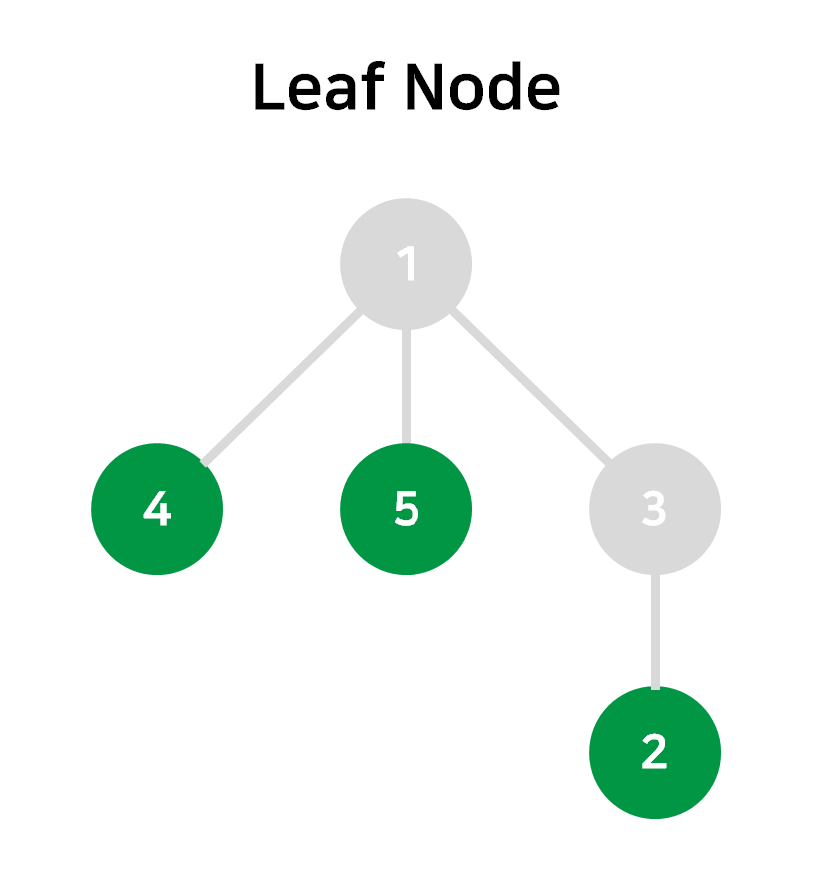
5. Leaf Node : Child 가 없는 단말 노드를 뜻한다.
   

---

키워드

이러한 구조를 가진 트리 문제들은 다양한 방식들로 나오지만 트리 구조의 조건을 대입해보면 알 수 있다.

다시 말하면, 모든 두 정점을 잇는 경로가 존재하며 사이클이 존재하지 않는 경우이다.

예를 들면 모든 마을이 연결되어 있고, 마을과 마을 사이를 연결하는 N - 1 개의 길이 있다고 가정하는 문제가 되겠다.

트리 문제를 풀 때는 문제의 어떤 것이 정점이고 간선인지 정확하게 정의해야 하고, 트리의 다양한 용어(Parent, Child, …)들이 문제와 어떻게 연결되는지 파악해야 한다.

---

저장 방법

그래프가 인접 행렬(Adjacency Matrix)과 인접 리스트(Adjacency List) 두가지 구조로 저장하기 때문에 트리도 이 두 방법을 사용할 수 있는데, 대부분의 경우 인접 리스트 구조로 저장을 하게된다.

그 이유는 공간 복잡도에 있는데, 인접 리스트는 공간 복잡도를 뜻하는 간선의 개수가 트리 구조로 인하여 $V(정점 개수) - 1$ 로 정해지는 반면, 인접 행렬 구조는 $V^2$ 이기 때문이다.

---

예시 문제

• BOJ 11725 - 트리의 부모 찾기, BOJ 1991 - 트리 순회, BOJ 5639 - 이진 검색 트리, BOJ 15900 - 나무 탈출, BOJ 20364 - 부동산 다툼, BOJ 3584 - 가장 가까운 공통 조상, BOJ 1240 - 노드 사이의 거리, BOJ 9489 - 사촌
• Subtree 문제 : 큰 문제와 작은 문제 개념을 이해하자. BOJ 1068 - 트리*(DP 미리보기), BOJ 15681 - 트리와 쿼리, BOJ 14267 - 회사 문화 1