JAVA 알고리즘 복습 3
서론
이 포스트는 코딩 테스트를 위해 수강했던 패스트캠퍼스의 알고리즘 강의 한 번에 끝내는 코딩테스트 369 Java편 초격차 패키지 Online. 의 류호석 강사의 강의를 복습하며 정리한 내용입니다.
알고리즘 분류
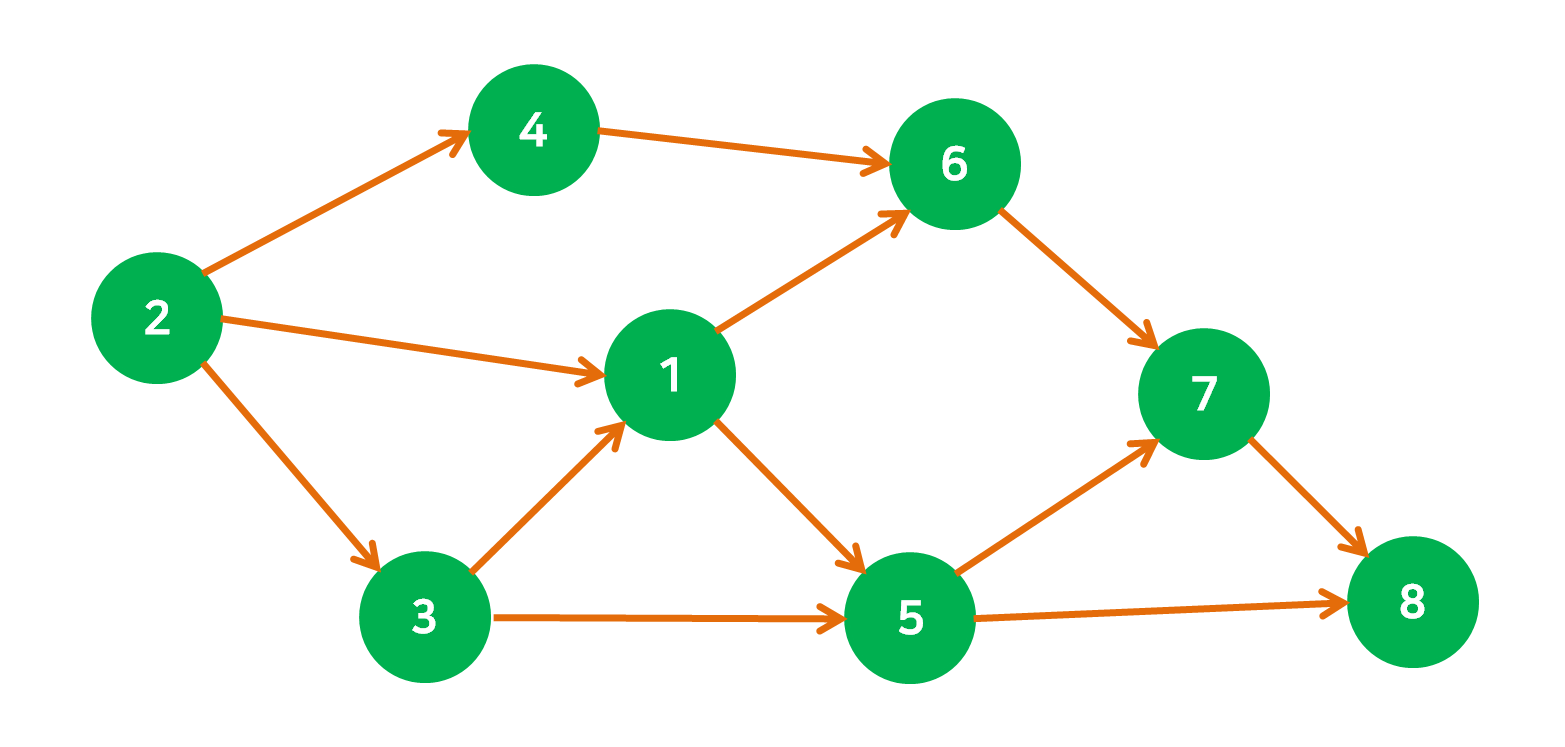
위상 정렬(Topological Sort)
위상을 기준으로 정렬한다는 뜻.
위상이 무엇인지 알기 위해서는 먼저 그래프 중에 DAG(Directed Acyclic Graph)에 대해서 알아야 한다.
DAG(Directed Acyclic Graph)
- Directed : 간선에 방향성이 존재한다.
- Acyclic : 사이클이 없다.
- Graph : 정점(V) + 간선(E) 으로 이루어져있다.
차수(Degree)
방향성이 없는 그래프에서는 정점에 연결된 간선의 수가 곧 차수를 뜻했다.
그러나 방향성이 존재하는 DAG 의 경우, 한 정점으로 들어오는 간선과 다른 정점으로 나가는 간선이 분리가 되므로, 두가지 종류의 차수를 사용한다.
- Indegree : 도착지가 자신(정점)인 간선의 개수
- Outdegree : 자신(정점)으로부터 나가는 간선의 개수
정렬 방법
이와 같은 간선, 즉 차수 정보를 사용하여 위상에 맞춰 정렬을 하는데 이러한 방법에는 크게 2가지 아이디어가 있다.
1. Indegree 를 사용한 정렬.
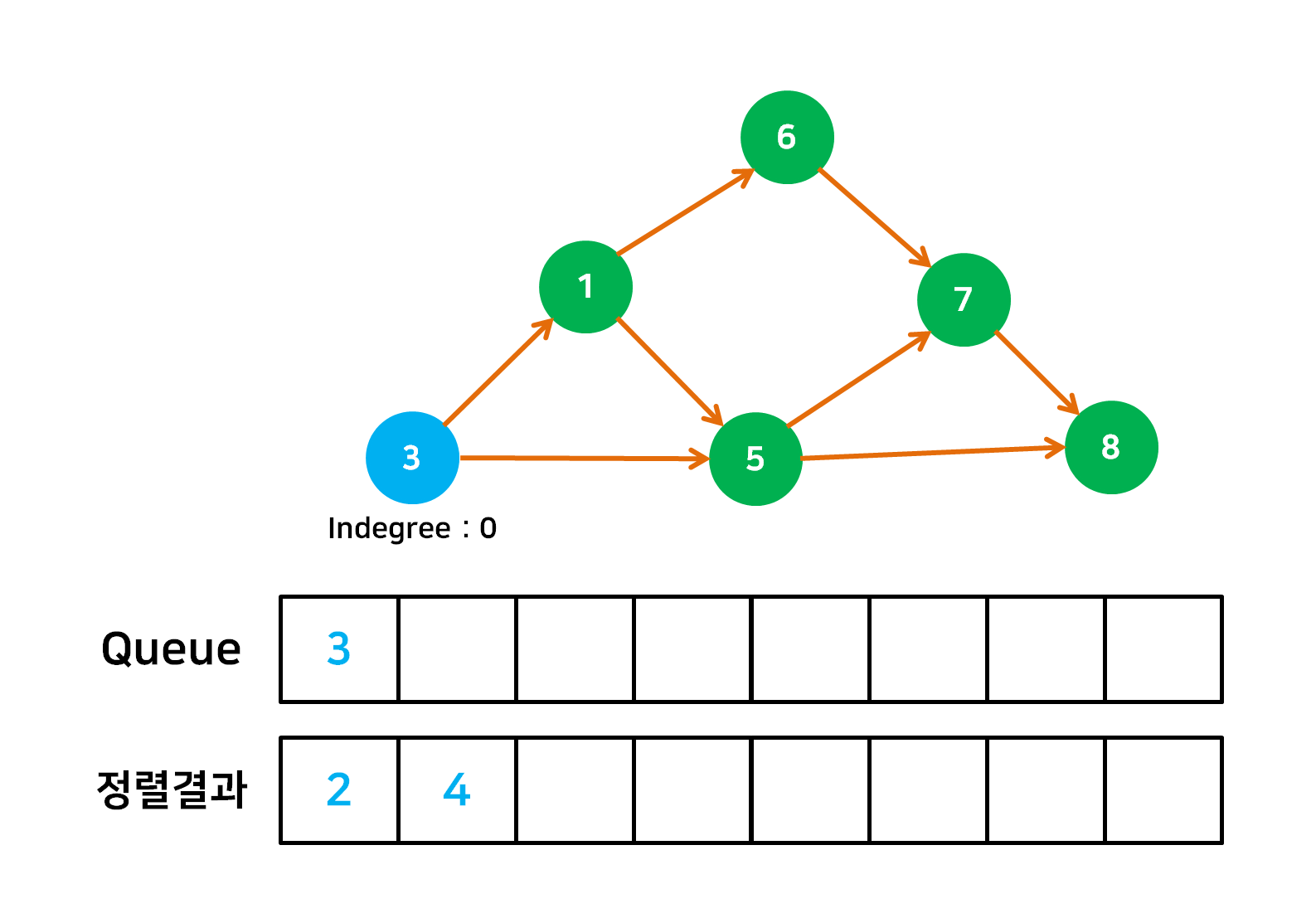
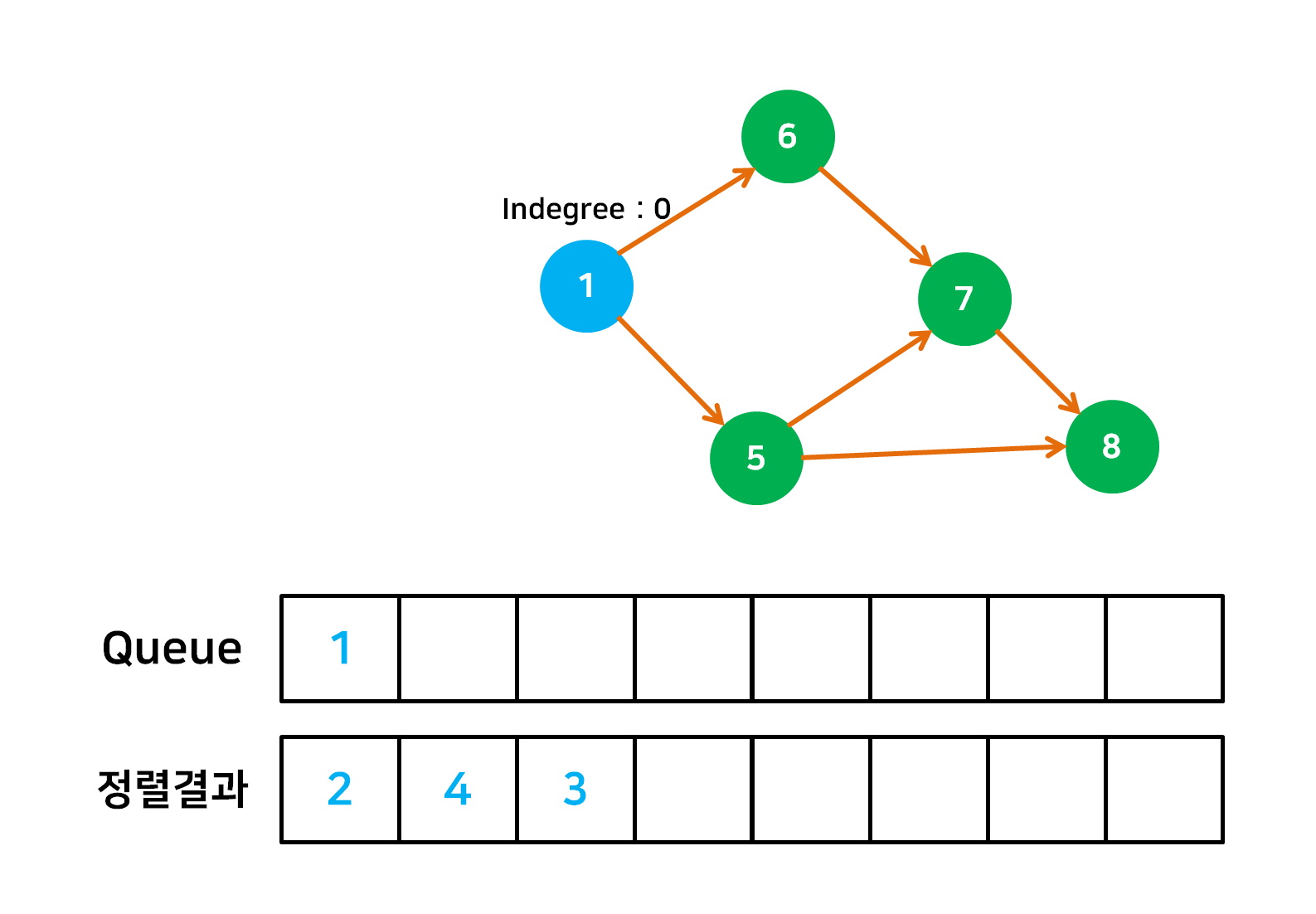
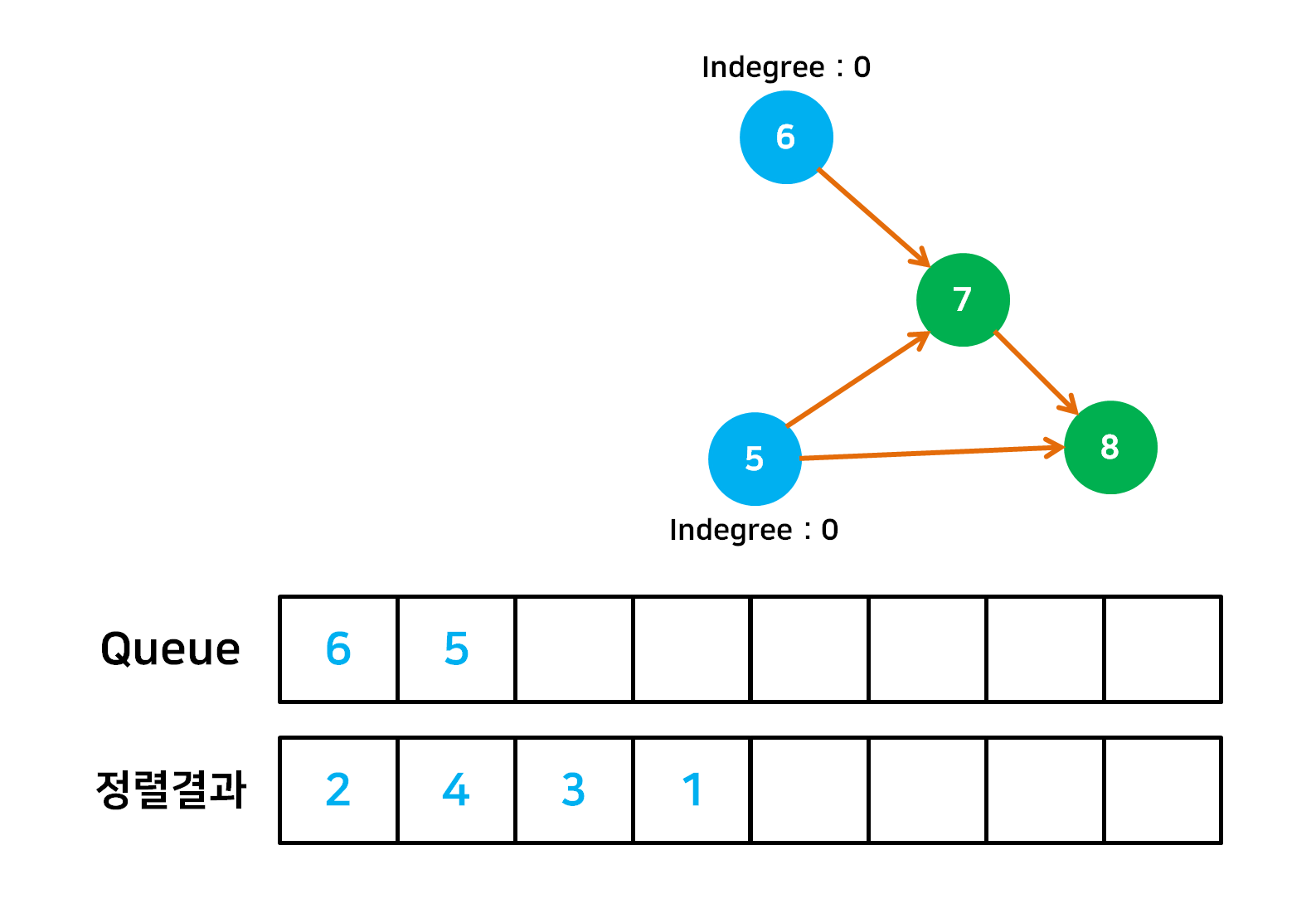
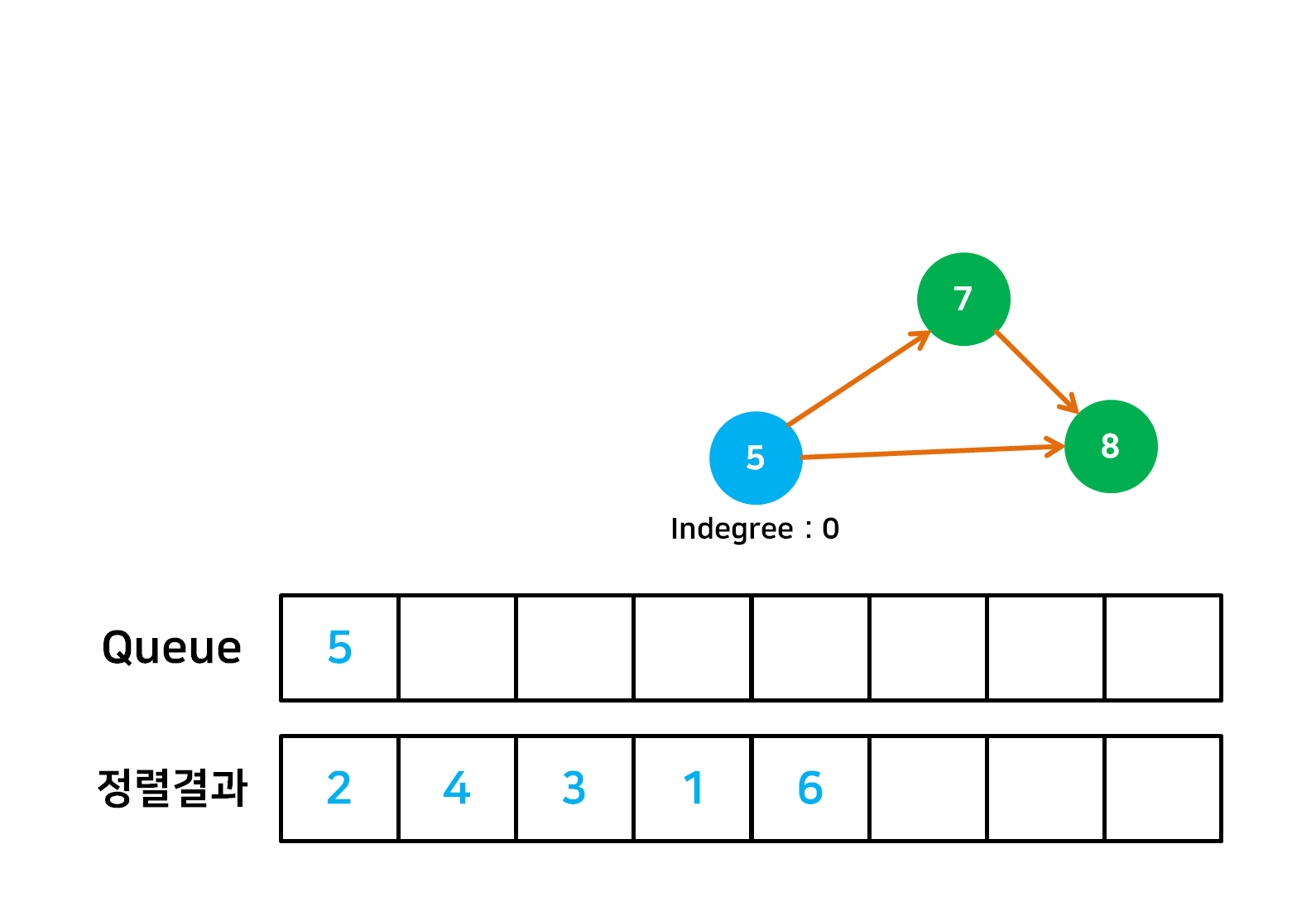
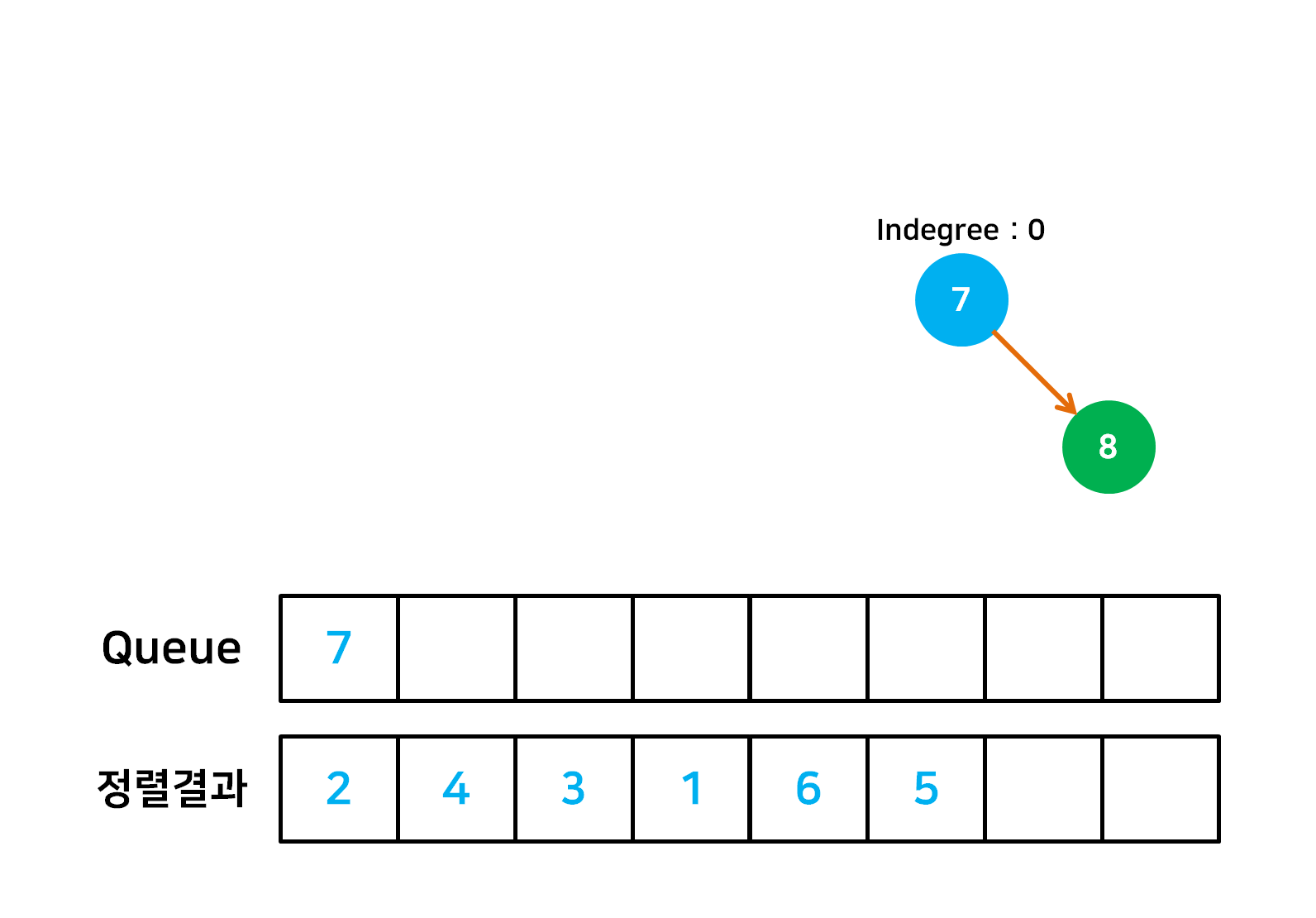
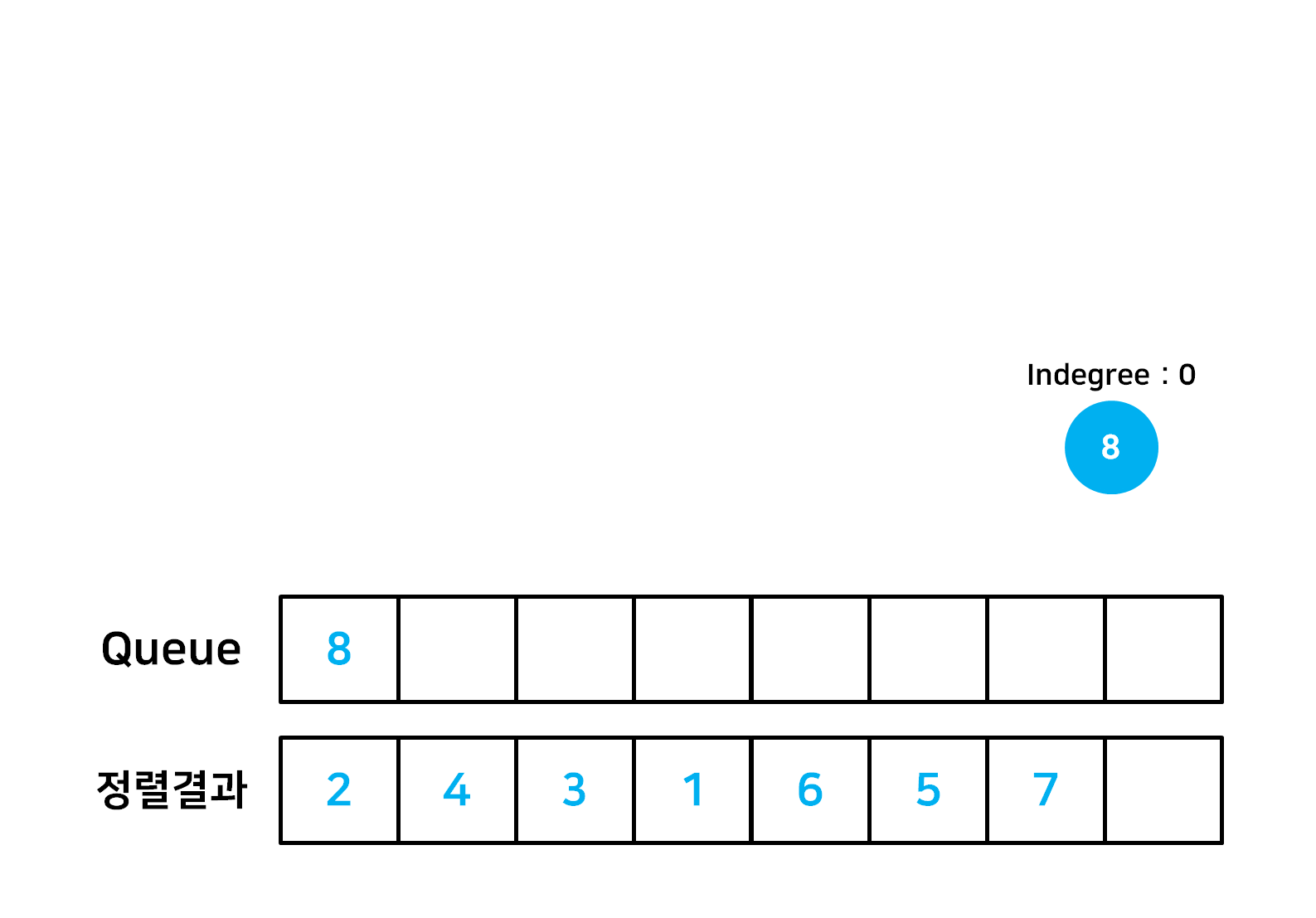
- 정렬의 시작점으로서 자신에게 들어오는 간선(Indegree)이 없는 정점을 Queue 에 넣는다.
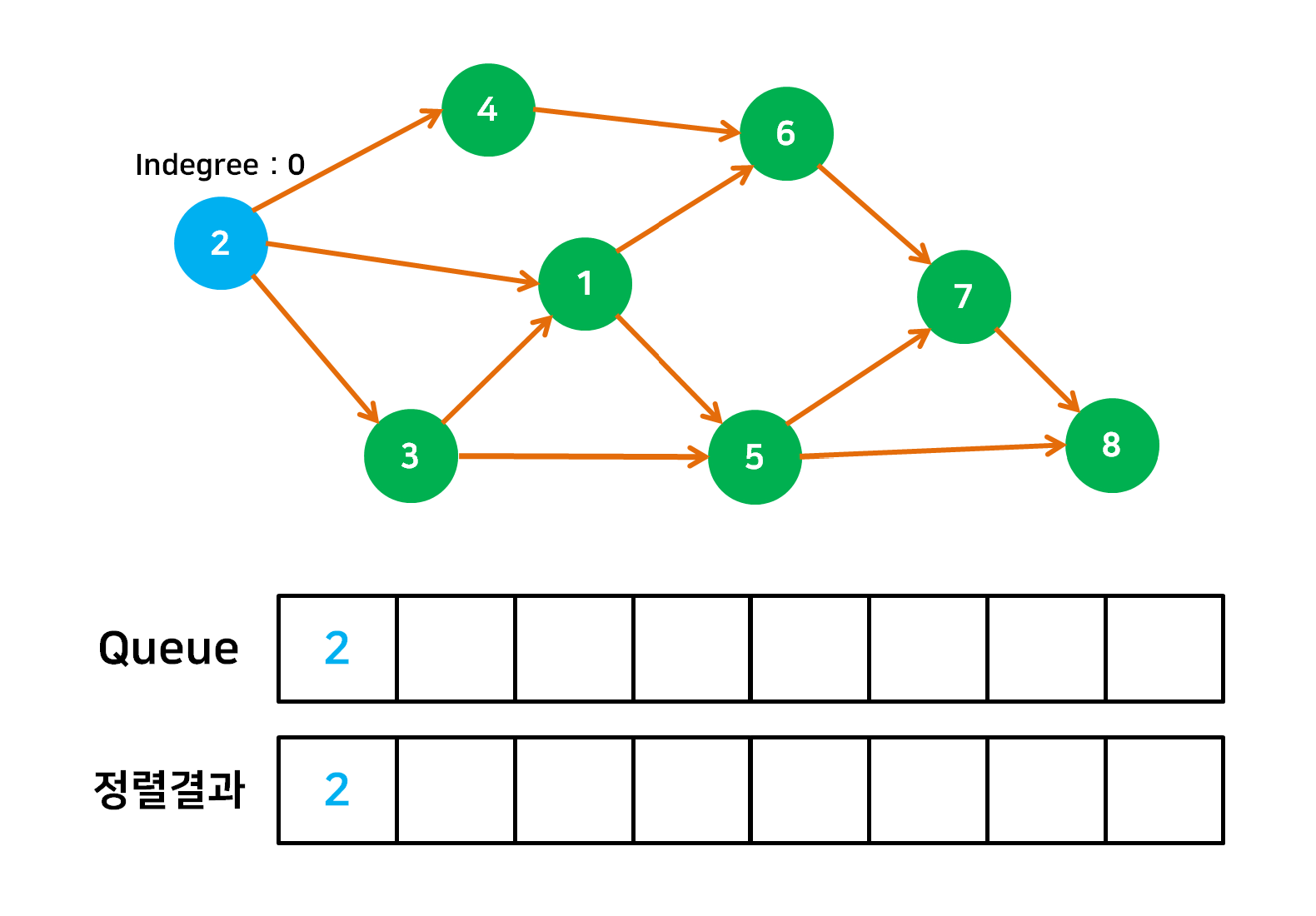
- Queue 의 첫 정점을 빼낸 후 정렬결과에 포함한 후에 outdegree 또한 삭제한다. 그 후 Indegree 가 0인 정점들을 다시 Queue 에 추가한다.
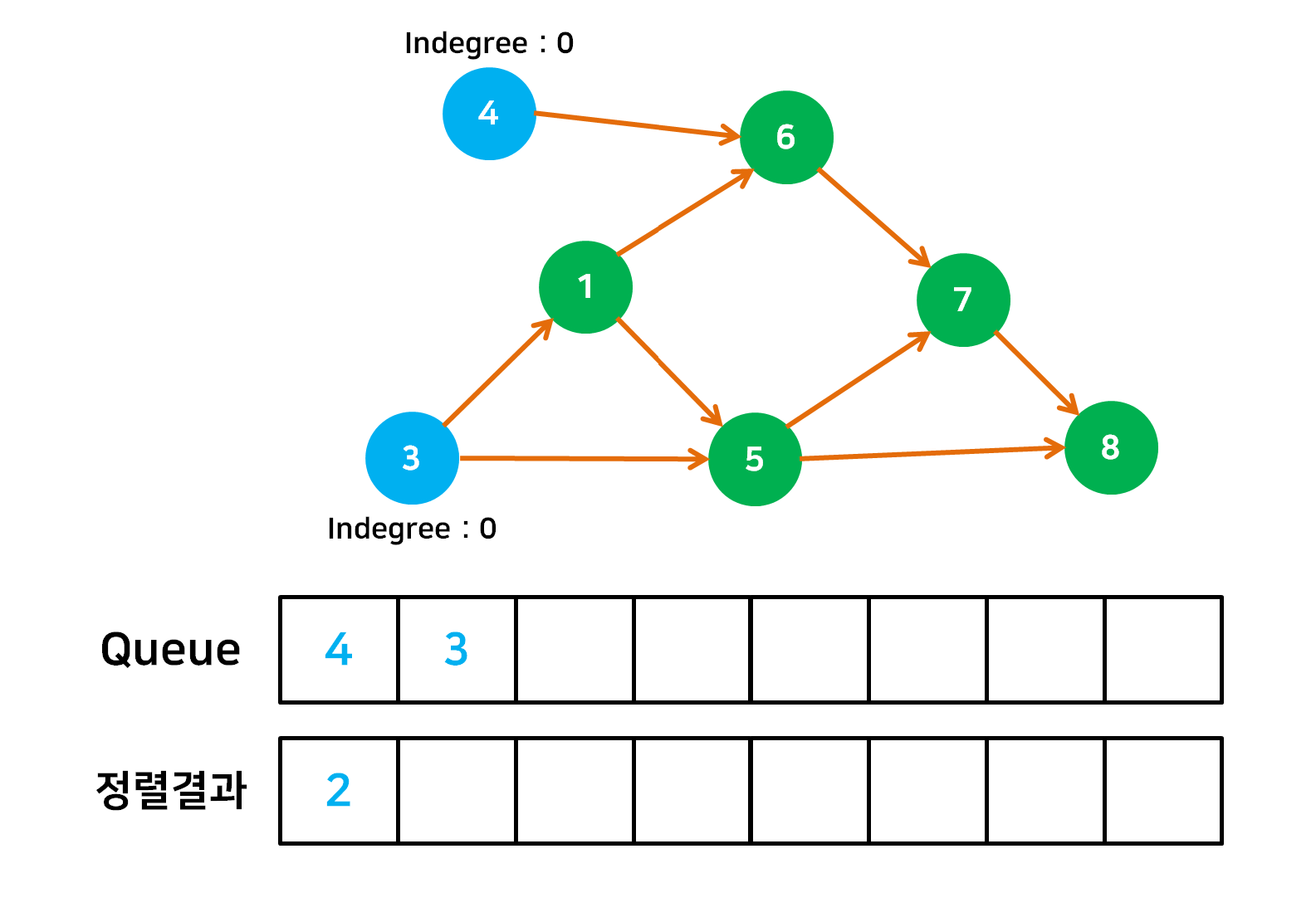
- Queue 가 빌 때 까지 2번의 작업을 계속 반복한다.

2. SCC(Strongly Connected Component)
이는 코딩테스트에는 나오지 않는 수준의 아이디어이므로 패스.
예시 문제
- BOJ 2252 - 줄 세우기, BOJ 2623 - 음악 프로그램, BOJ 9470 - Strahler 순서, BOJ 14676 - 영우는 사기꾼?
- BOJ 1005 - ACM Craft, BOJ 1516 - 게임 개발, BOJ 2056 - 작업, BOJ 2637 - 장난감 조립
최단 경로(Shortest Path)
최단거리란?
그래프의 시작점에서 다른 지점까지의 최단 거리를 뜻한다.
최단 거리를 구하는 방식은 여러가지가 있다.
| 이름 | 간선 가중치 | 시작점 | 도착점 | 시간 복잡도 |
|---|---|---|---|---|
| BFS | 1 | 1개 | V(모든 정점) | $O(V + E)$ |
| Dijkstra | 0 이상 | 1개 | V(모든 정점) | $O(E\log{V})$ |
| Floyd-Warshall | 제약 없음 | V(모든 정점) | V(모든 정점) | $O(V^3)$ |
| Bellman-Ford | 제약 없음 | 1개 | V(모든 정점) | $O(V*E)$ |
| SPFA | 제약 없음 | 1개 | V(모든 정점) | $O(V*E)$ |
| A* | 0 이상 | 1개 | 1 | $O(b^d)$ |
위 방식중에서도 코딩 테스트에는 BFS, Dijkstra 알고리즘이 주로 나온다.
Dijkstra 를 알아보기 전에, 그래프에서의 탐색을 리마인드 해보자.
탐색이란 시작점에서 0개 이상의 간선을 거쳐 갈 수 있는 정점들을 찾는 것이다.
대표적인 방식으로 앞서서 DFS, BFS 를 배웠다.
BFS 의 경우에는 간선의 가중치가 동일할 때, 최소 이동 횟수로 최단거리를 계산할 수 있었다.
이제 다익스트라 알고리즘은 어떻게 탐색을 하는지 알아보자.
다익스트라(Dijkstra) 알고리즘
먼저 다익스트라 알고리즘을 사용하기 위해서는 다음 항목들을 고려해야 한다.
Input
- 가중치가 0 이상인 간선들로 이루어진 그래프($G(V, E)$)
- 시작 정점 $S$ or 시작 정점들 $\lbrace S_1, … \rbrace$
Output
- 시작 정점 $S$ 로 부터 모든 정점까지의 최단 거리
시간 복잡도
시간 복잡도는 $O(E\log{V})$ 이다.
그 외에도 탐색에 필요한 두가지 자료구조를 사용한다.
- $dist[i]$ : 시작 정점 $S$ 에서 $i$ 번 정점까지의 최단 거리를 저장한 배열
- $D$ : $\lbrace (v, d) \rbrace$( = 시작 정점 $S$ 에서 정점 $v$ 까지 가중치 $d$ 를 통해 갈 수 있다는 정보) 들을 저장하는 자료구조.
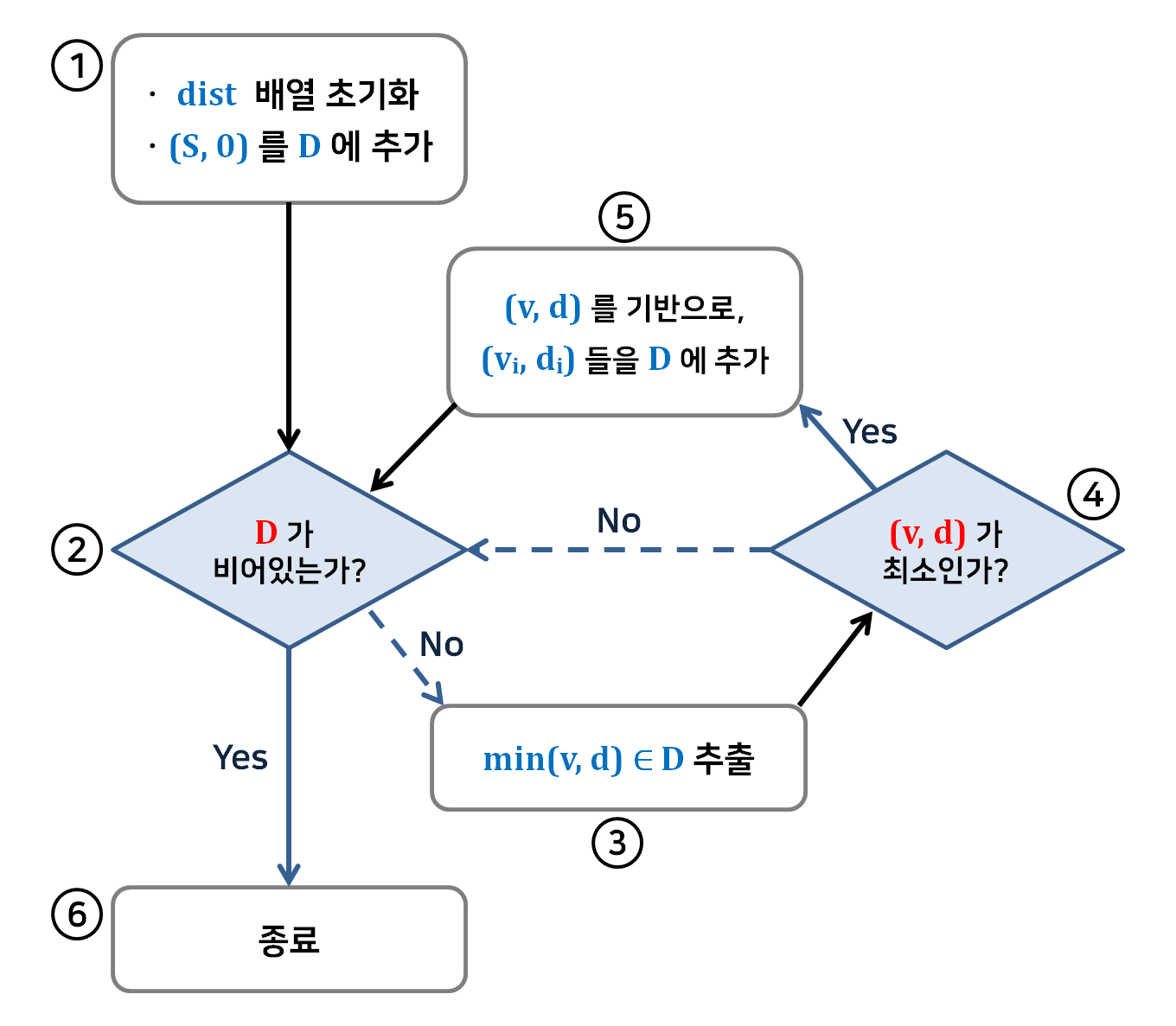
순서도
다익스트라 알고리즘의 동작을 순서도로 표현하면 다음과 같다.
번호별로 동작을 살펴보자.
- ㆍ$dist$ 배열은 시작 정점은 0, 나머지 정점들은 최대값으로 설정한다.
ㆍ$D$ 에는 $(S, 0)$ 을 추가한다. - $D$ 가 비어있는지 체크한다.
- $D$ 에서 최단 거리 d 를 갖는 데이터 $(v, d)$ 를 추출한다.
- 추출한 최단 거리 데이터 $(v, d)$ 가 $dist[v]$ 에 저장된 최단거리보다 짧은지 확인한다.
(더 큰 경우, 실제 최단거리가 아니기 때문에 가치가 없는 정보이므로 폐기한다.) - $(v, d)$ 가 최단 거리가 맞다면, 이를 기반으로 $v$ 에 연결된 간선들을 보고 연결된 정점으로의 거리 데이터 $(v_i, d_i)$ 들을 $D$ 에 추가한다.
- 더이상 D에 정보가 없으면 종료한다.
시간 측면에서 살펴보면 3번 과정에서 $D$ 로부터 원소를 추출하고, 5번 과정에서 $D$ 로 원소를 추가한다.
추출 횟수는 추가 횟수 이하일 수 밖에 없고, 추가하는 횟수의 최대값은 모든 정점의 차수(= 연결된 간선의 개수)의 합과 같다.(모든 정점은 최대 한 번씩 가치가 있는 v 로 사용된다.)
\[N(추가) \approx deg(1) + deg(2) + ... deg(V) = \|E\|\]이제 3번, 5번 과정에 걸리는 시간 $T(3)$, $T(4)$ 를 알면 된다.
이는 $D$ 를 구현할 때 어떤 자료구조를 사용하는지에 따라 달라진다.
1차원 배열의 경우 추가는 1 의 시간복잡도로 매우 빠르지만, 최소값을 추출하는데 전체를 살펴봐야 하므로 N 의 시간복잡도를 가진다.
Min Heap 이나 Priority Queue 같은 경우 추가와 추출(poll 시 최소값이 추출됨) 모두 $\log{E}$ 의 시간 복잡도를 가진다.
다익스트라 알고리즘의 시간복잡도를 표현하자면 아래와 같다.
\[T(전체 시간) \le [T(5) + T(3)] * E\]이처럼 두 종류의 시간 합을 사용할 때, 한쪽이 작더라도 다른 한쪽이 매우 크면 결과적으로 더 커질 수 밖에 없다.
따라서 한쪽만 아주 작은 것 보다, 전체적으로 작은 것이 더 낫다.
이러한 관점에서 1차원 배열 보다는 Min Heap / Priority Queue 가 더 적합하다.
따라서 $O(E \log{E})$ 의 시간 복잡도를 가지게 되는데, $E$ 는 $V^2$ 이하일 수 밖에 없다. $\log$ 에서 제곱은 2배밖에 안되므로, 결국 3~5 과정은 최대 $O(E \log{V})$ 로 표현이 가능하다.
예시 문제
Floyd-Warshall
다익스트라가 한 정점에서 다른 정점으로의 최단 거리를 구한다면, Floyd-Warshall 은 모든 정점에서 모든 정점으로의 최단 거리를 구한다.
Floyd-Warshall 의 알고리즘을 간단하게 식으로 표현하면 다음과 같다.
$D_{ab} = min(D_{ab} \ , \ D_{ax} + D_{xb})$
이러한 식을 점화식이라고 하며, 이는 DP 알고리즘에서 사용되는 개념이다. DP 에 대해서는 다음장에서 다룰 예정이므로 일단은 점화식이 무엇인지 감만 잡고 넘어가자.
점화식이 표현하는 바는 다음과 같다. N개의 정점을 각각 목적지에 도달하기 위한 경유지 역할로 사용한다. 이 경유지를 거치지 않은 노드간의 거리와 경유지를 거친 경우의 거리 중 더 짧은 거리를 최단거리 배열 D 에 저장한다.
예시
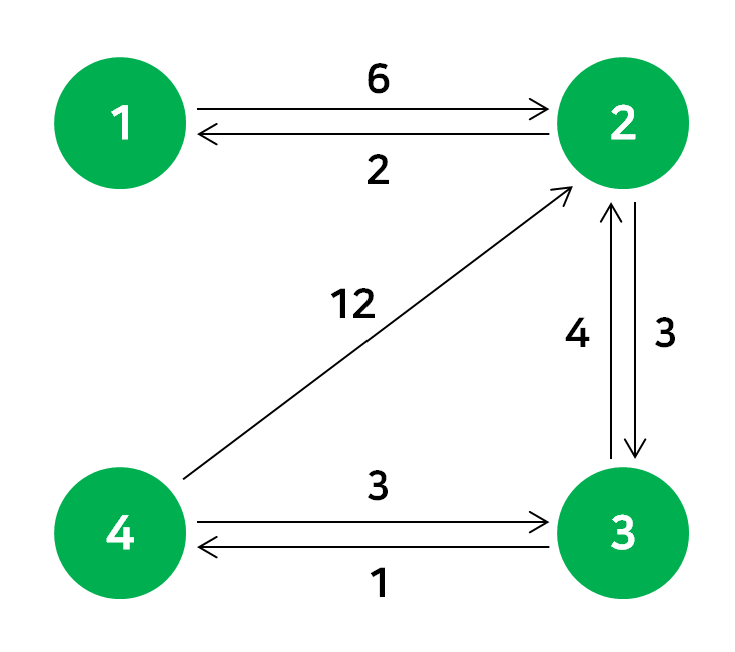
이에 대한 간단한 예시를 살펴보자.
아래의 그림은 4개의 정점과 간선들로 표현된 그래프이다.
이 그래프의 내용으로 Floyd-Warshall 알고리즘이 어떻게 동작하는지 살펴보자.
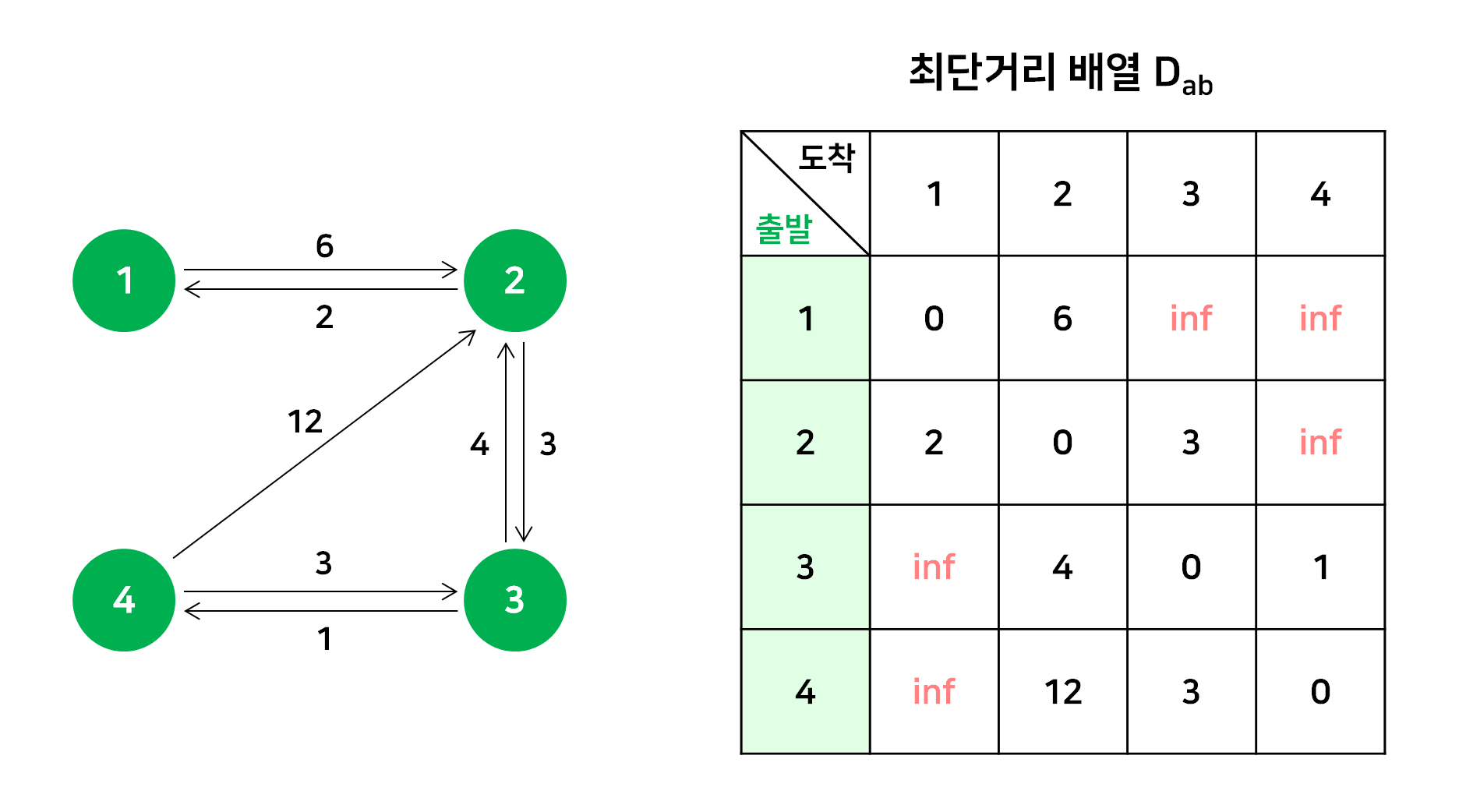
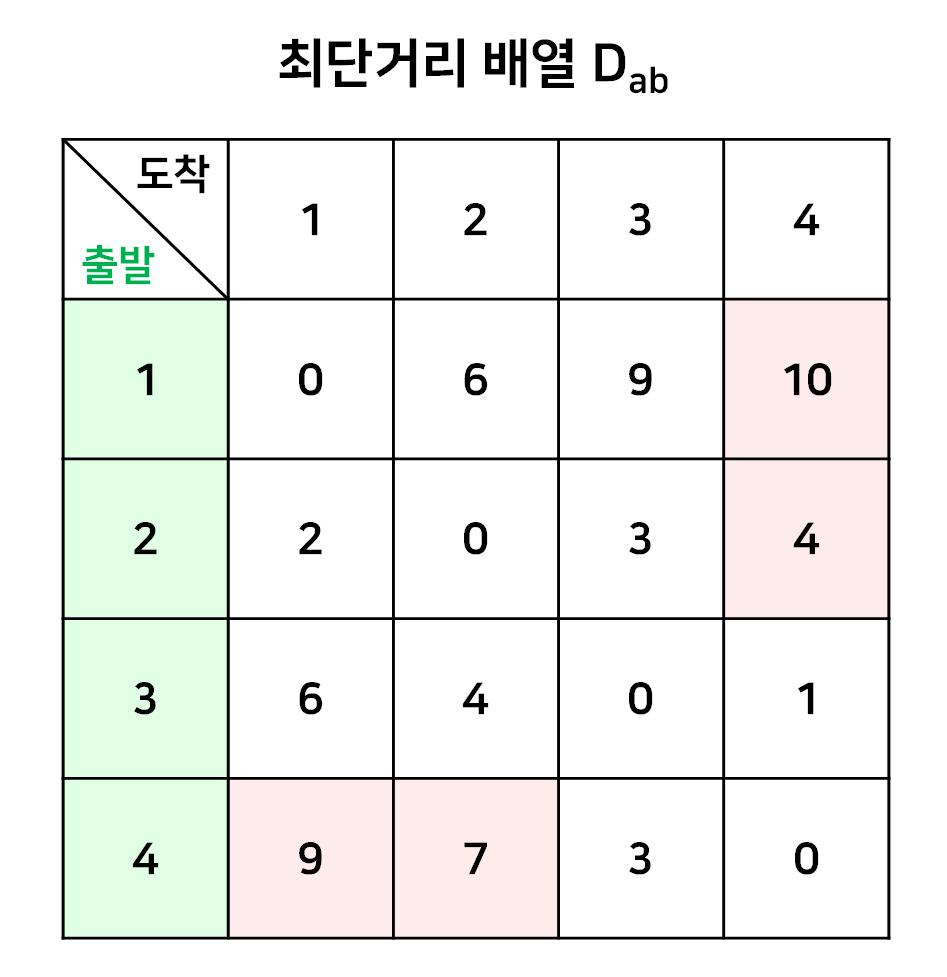
먼저 각 정점끼리의 최단거리 배열을 초기화하는데, 이는 주어진 간선의 정보를 사용한다. 출발점과 도착점 2가지를 기준으로 정보를 저장하기 때문에 2차원 배열을 사용한다.
이러한 배열을 초기화할 때, 출발 정점과 도착 정점이 같으면 비용이 0 이고, 정점간의 이동경로가 없는 경우 비용을 무한대(inf) 로 저장한다.
이에 따라 배열을 초기화하면 다음과 같다.
이제 모든 정점간의 최단 거리를 갱신하기 위해서 각 정점을 경유지로 설정하고 배열의 정보를 갱신해보자.
먼저 1번 정점을 경유지로 설정하는 경우, 갱신할 수 있는 이동 경로는 다음과 같다.
경유지 : 1번 정점
보면 알겠지만 굉장히 단순한 방식을 사용한다. 안타깝게도 1번 정점을 경유하는 경우 갱신되는 최단거리 값이 없다.
이제 마찬가지로 나머지 2, 3, 4번 정점에 대해서 같은 작업을 반복한다.
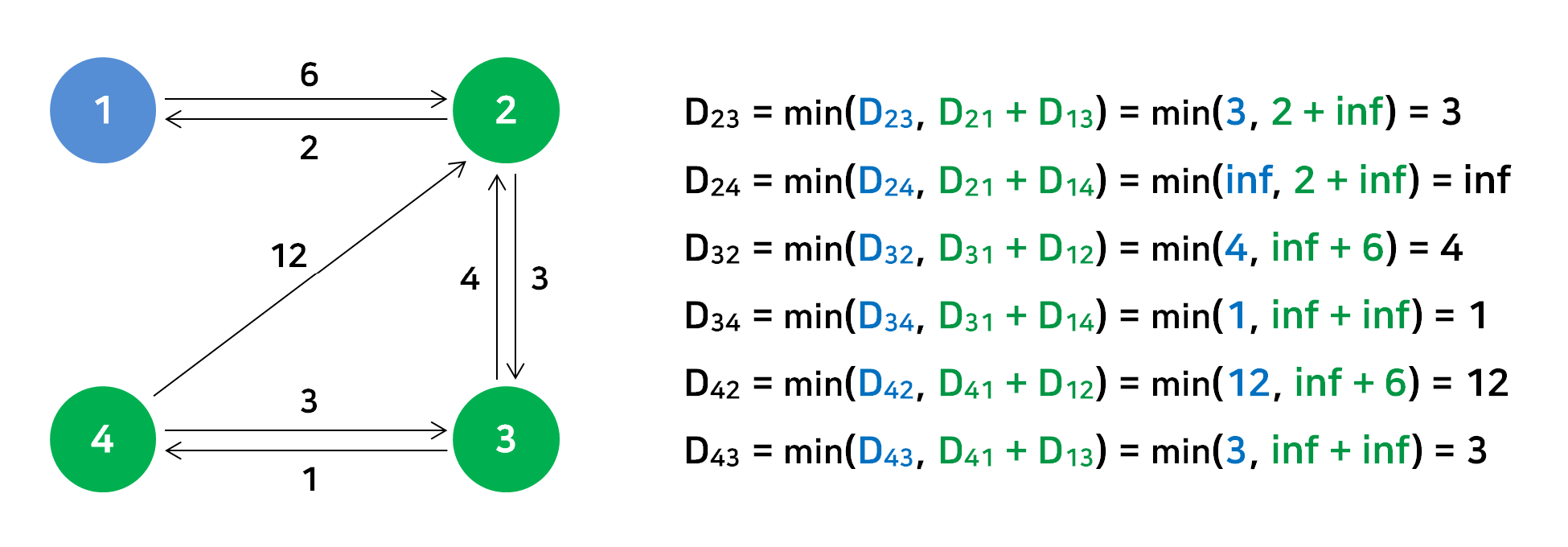
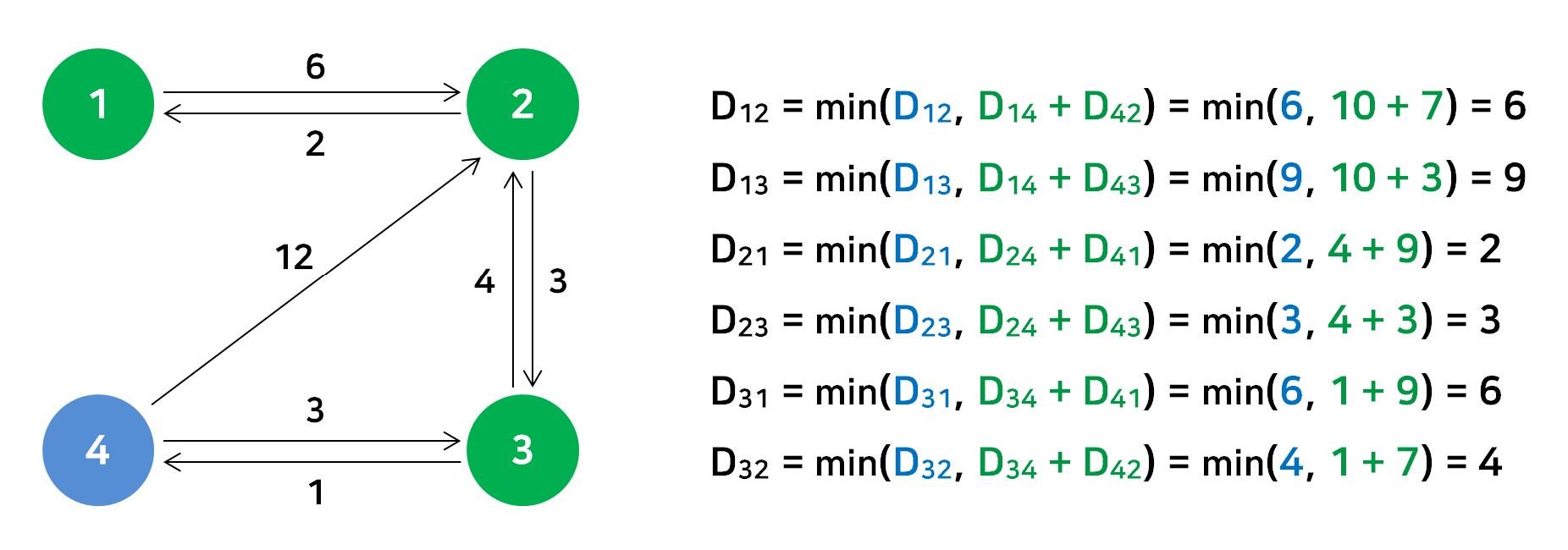
경유지 : 2번 정점
드디어 갱신할 최단거리가 생겼다. 이 정보를 배열에 저장하자.
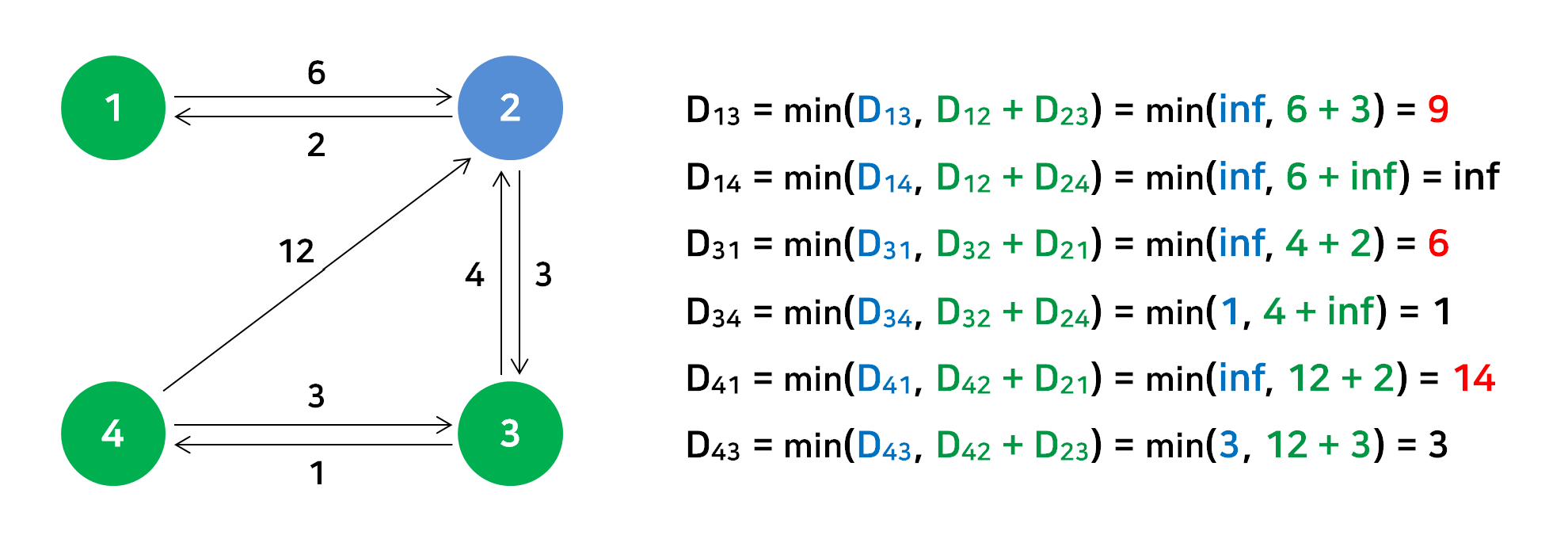
경유지 : 3번 정점
최단거리 배열을 갱신한다.
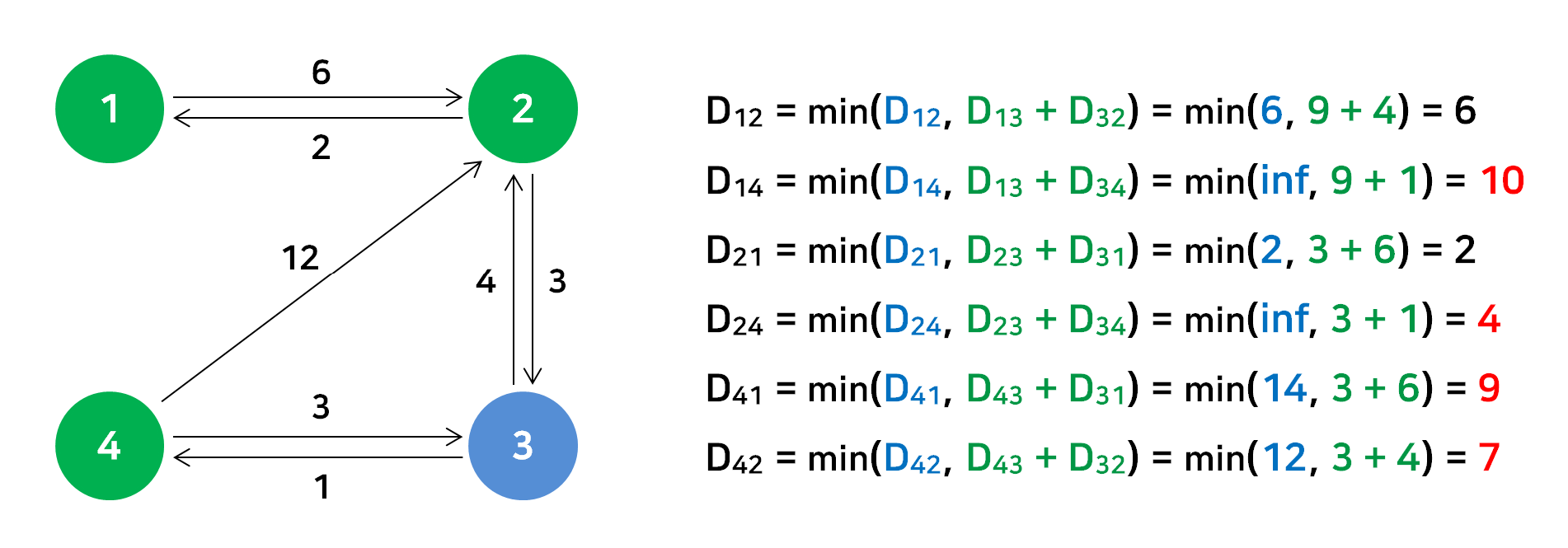
경유지 : 4번 정점
변화된 최단거리가 없다.
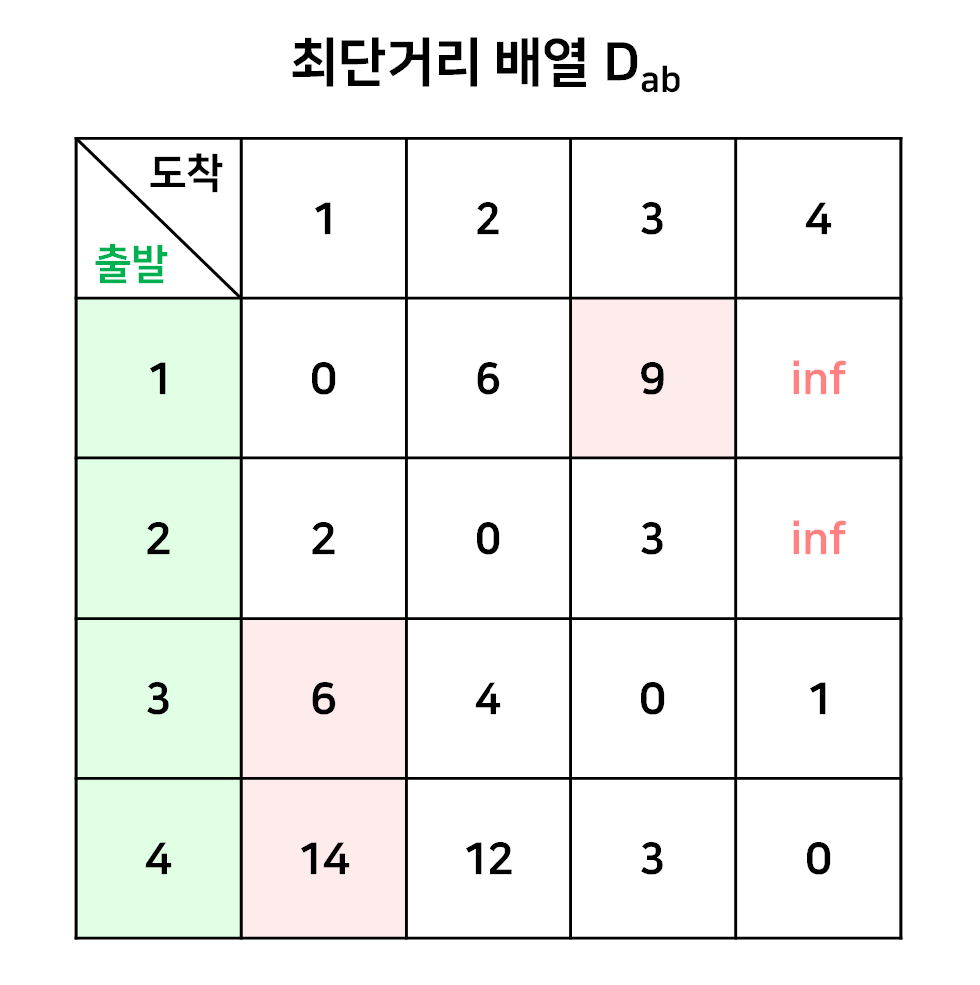
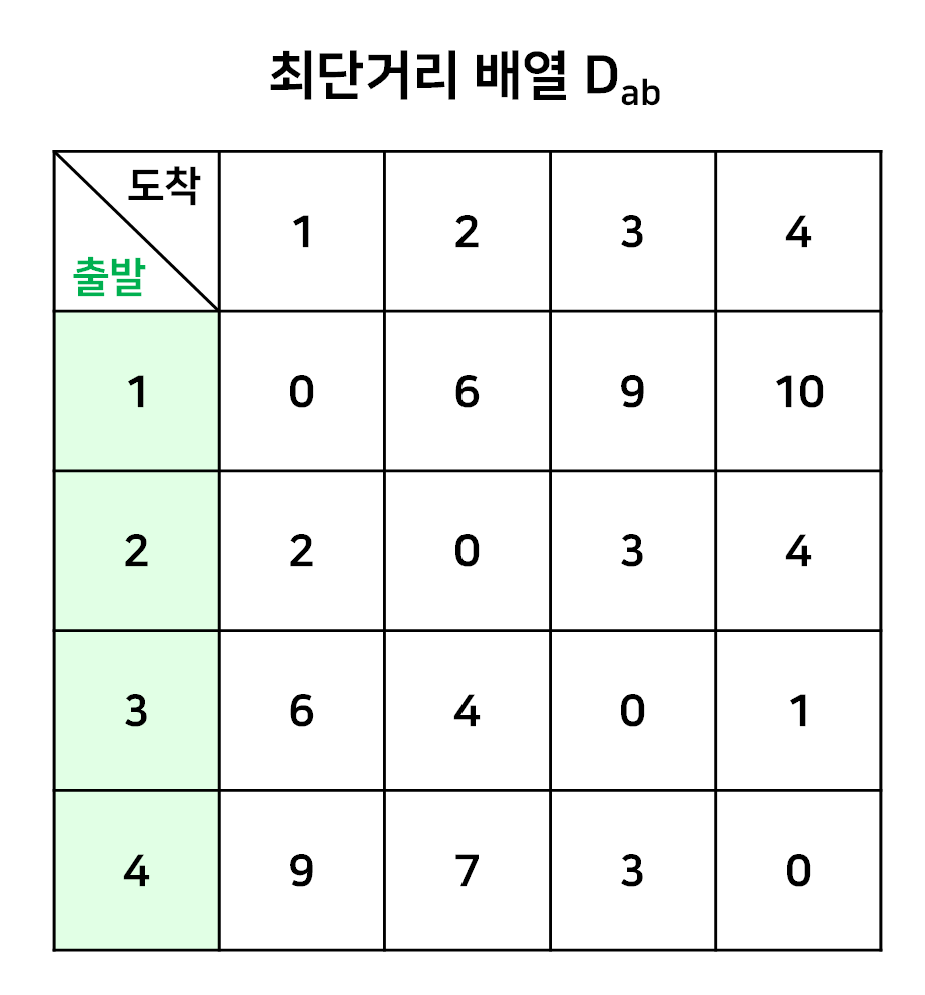
이제 최종적으로 완성된 최단거리 배열은 다음과 같다.
방식 자체는 단순하지만 수행하는데 걸리는 시간을 살펴보면 다음과 같다.
먼저 모든 정점을 경유지로 사용하고(N), 경유지를 제외한 다른 정점들을 시작점으로 사용한다.(N - 1) 마지막으로 각각의 시작점에 대해 경유지를 제외한 도착점들에 대해 최단거리를 찾는다.(N - 2)
따라서 시간 복잡도는 다음과 같다.
$O(N(N-1)(N-2)) \approx O(N^3)$
모든 정점에 대한 최단 거리를 찾는 만큼 다익스트라보다 훨씬 높은 시간 복잡도를 갖는다.