JAVA 알고리즘 복습 4
서론
이 포스트는 코딩 테스트를 위해 수강했던 패스트캠퍼스의 알고리즘 강의 한 번에 끝내는 코딩테스트 369 Java편 초격차 패키지 Online. 의 류호석 강사의 강의를 복습하며 정리한 내용입니다.
알고리즘 분류
동적 프로그래밍(DP;Dynamic Programming)
Dynamic 의 뜻은 동적인, 변화하는 이라는 뜻을 가진다.
Dynamic Programming 이란, 문제의 크기를 변화하면서 정답을 계산하는 방법이다.
간단히 말하면 작은 문제의 결과를 이용해 큰 문제의 정답을 빠르게 계산하는 방법이라고 보면 된다.
DP 의 사용 기준?
- 문제 풀이에 완전 탐색(Brute-Force Search)을 먼저 시도해본다.
- 완전 탐색으로는 경우의 수가 지나치게 많다고 판단되면 DP 를 시도해볼 수 있다.
DP 의 순서
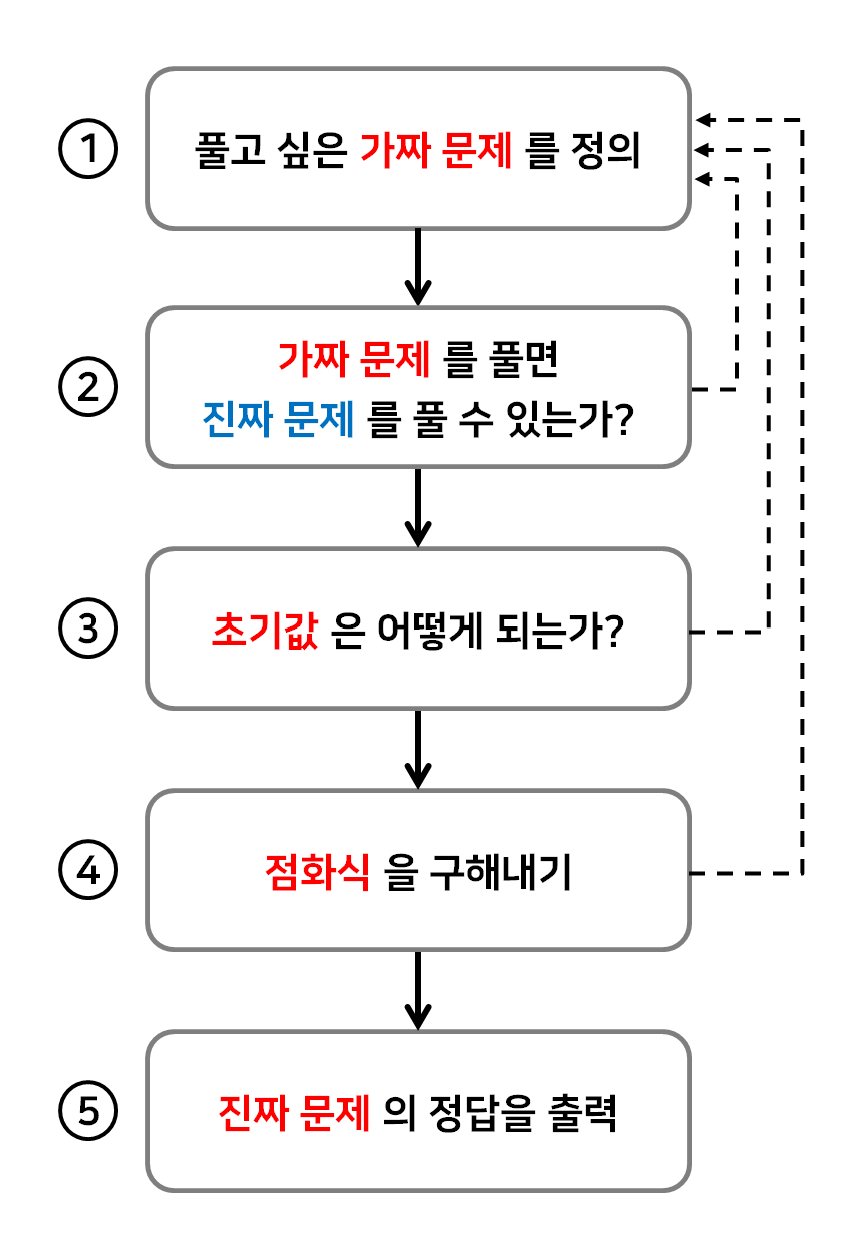
DP 의 경우, 문제 풀이의 과정을 규격화하여 푸는것이 좋은데, 강의에서 제안하는 순서도는 다음과 같다.
한 단계씩 살펴보자.
1. 풀고 싶은 가짜 문제를 정의
여기서 가짜 문제란 사이즈를 바꾼 문제를 뜻한다.
이 경우 다음과 같은 정의 예시가 있다.
Dy[i]: 1 ~ i 번째 원소에 대해 조건을 만족하는 경우의 수Dy[i][j]: 두 종류로 정의 가능- i ~ j 번째 원소에 대해 조건을 만족하는 최댓값
- 수열
A[1...i]와 수열B[1...j]에 대해서 무언가를 계산한 값
2. 가짜 문제를 풀면 진짜 문제를 풀 수 있는가?
가짜 문제를 정의하고 바로 풀이하는 것이 아니라, 이를 통해 진짜 문제를 풀 수 있는지 확인해야 한다.
다음 예시를 살펴보자.
- 진짜 문제
- 수열
A[1...N]에서 조건을 만족하는 부분 수열의 개수 - 가짜 문제
Dy[i]: 수열A[1...i]에서 조건을 만족하는 부분 수열의 개수
이 경우, 가짜 문제를 풀어서 Dy[1], Dy[2], …, Dy[N] 까지 모두 채워 넣었을 때, Dy[N] 이 곧 진짜 문제가 원하는 값이므로 진짜 문제를 풀 수 있다고 본다.
진짜 문제를 풀 수 없는 경우, 다시 1번으로 돌아가서 가짜 문제를 정의한다.
3. 초기값은 어떻게 되는가?
초기값은 더이상 쪼갤 수 없는 가장 작은 문제를 해결함으로서 설정된다.
가짜 문제를 설정할 때 문제를 쪼개는 이유는 문제가 너무 크기 때문인데, 문제가 충분히 작고 빨리 풀 수 있다면 더이상 쪼갤 필요가 없기 때문에 초기값으로 설정한다.
초기값을 제대로 설정할 수 없으면 다시 1번으로 돌아간다.
4. 점화식을 구해내기
큰 문제가 작은 문제를 어떻게 이용하는지를 구해낸다.
이를 점화식을 구해낸다 라고 표현한다.
이러한 점화식을 구할 수가 없다면, 특정 조건을 빼먹는 등 오류가 있다는 뜻이기 때문에 다시 1번으로 돌아간다.
5. 진짜 문제의 정답을 출력
위 과정을 거쳐서 채워진 Dy 테이블을 이용해 진짜 문제의 정답을 찾아낸다.
DP의 장단점
- 장점
- 규격화된 형태가 있다.
- 성공하기만 하면 코딩량이 적고 시간 복잡도 또한 $O(N)$ 으로 매우 빠르다.
- 규격화된 형태가 있다.
- 단점
- 가짜 문제를 찾아내고 점화식을 만들어야 하기 때문에 어렵다.
예시 문제
연습 문제
- BOJ 1003 - 피보나치 함수, BOJ 10870 - 피보나치 수 5, BOJ 15988 - 1, 2, 3 더하기 3, BOJ 15991 - 1, 2, 3 더하기 6, BOJ 11052 - 카드 구매하기, BOJ 2011 - 암호 코드
잘못된 점화식을 수정하는 예시
문제의 정의는 다음과 같다.
계단을 밟으며 올라가서 N번재 계단까지 가야 한다. 다음의 조건을 참조해서 최대 점수를 구하자.
- 계단은 한칸 또는 두칸 간격으로 오를 수 있다.
- 단, 계단을 세칸 연속으로 밟을 수 없다.
- 각 계단에는 밟을 때 얻는 점수가 있다.
- 마지막 계단은 반드시 밟아야 한다.
계단은 최대 300개 까지 가능하므로, 완전 탐색을 사용하기에는 시간이 모자라다.(1과 2의 순열 중에서 1이 연속으로 최대 2개까지만 이어지고, 총합이 300이 되는 경우의 수는 chatgpt에게 물어본 결과 4,335,644,042,822,116,643,612,823,121,644,110,901,353,836,617,951,231,500개 라고 하니 다른 방법을 찾아야겠지?)
이 문제를 풀기 위해서 일단 간단하게 가짜 문제를 정의해보자.
1. 가짜 문제 정의
일단 도전해보고 안되면 고치면 된다.
- 진짜 문제
- N 번째 계단에 도착하며 얻는 최대 점수
- 가짜 문제
Dy[i]: i 번째 계단에 도착하며 얻는 최대 점수
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| A[i] | 0 | 10 | 20 | 15 | 25 | 10 | 20 |
| Dy[i] | ? | ? | ? | ? | ? | ? | ? |
2. 가짜 문제로 진짜 문제를 풀 수 있는가
Dy 테이블만 채우면 Dy[N] 이 곧 정답이다.
3. 초기값
쪼개지 않아도 풀 수 있는 작은 문제.
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| A[i] | 0 | 10 | 20 | 15 | 25 | 10 | 20 |
| Dy[i] | 0 | ? | ? | ? | ? | ? | ? |
4. 점화식 구하기
Dy[i]계산에 필요한 탐색 경우를 공통점끼리 묶기(Partitioning)- 한칸을 올라가서 i 번째에 온 경우
- 두칸을 올라가서 i 번째에 온 경우
- 묶어낸 부분의 정답을 Dy 테이블을 이용해 빠르게 계산하기
- Dy[i] = (i - 1) 번째 계단 최대 점수 + A[i]
- Dy[i] = (i - 2) 번째 계단 최대 점수 + A[i]
이러면 Dy[i] = Dy[i-1] + A[i], Dy[i] = Dy[i-2] + A[i] 를 사용하면 되겠지??
.
.
.
.
.
☠️ 틀렸다.
Dy[i-1] 에는 i - 1 번째 계단에 어떻게 도착했는지에 대한 정보가 없기 때문에, 세 계단을 연속해서 밟는 경우를 제외하지 못하기 때문이다.
문제를 풀면서 점화식을 만들다보면 이러한 오류가 생기는 것은 당연하다.
이 때, 오류의 원인인 모자란 정보를 Dy 에 추가시키는 방향으로 수정을 해야한다.
이 문제에서는 이전의 계단을 밟았는지 아닌지에 대한 정보가 모자라서 오류가 발생했다. 해당 정보를 추가해서 가짜 문제를 다시 정의해보자.
1. 가짜 문제 정의
- 진짜 문제
- N 번째 계단에 도착하며 얻는 최대 점수
- 가짜 문제
- Dy[i][0] : i - 1 번째 계단을 밟지 않고, i 번재 계단에 도착하며 얻는 최대 점수
Dy[i][1] : i - 1 번째 계단을 밟고, i 번재 계단에 도착하며 얻는 최대 점수
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| A[i] | 0 | 10 | 20 | 15 | 25 | 10 | 20 |
| Dy[i][0] | ? | ? | ? | ? | ? | ? | ? |
| Dy[i][1] | ? | ? | ? | ? | ? | ? | ? |
2. 가짜 문제로 진짜 문제를 풀 수 있는가
Dy 테이블만 채우면 $max(Dy[n][0], Dy[N][1])$ 이 곧 정답이다.
3. 초기값
쪼개지 않아도 풀 수 있는 작은 문제.
세 번째 계단부터는 같은 방식으로 계산이 가능하므로, 두 번째 계단까지 계산을 해보자.
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| A[i] | 0 | 10 | 20 | 15 | 25 | 10 | 20 |
| Dy[i][0] | 0 | 10 | 20 | ? | ? | ? | ? |
| Dy[i][1] | 0 | 0 | 30 | ? | ? | ? | ? |
4. 점화식 구하기
Dy[i]계산에 필요한 탐색 경우를 공통점끼리 묶기(Partitioning)- 한칸을 올라가서 i 번째에 온 경우
- 두칸을 올라가서 i 번째에 온 경우
- 묶어낸 부분의 정답을 Dy 테이블을 이용해 빠르게 계산하기
- Dy[i][0] = (i - 2) 번째 계단의 최대 점수 + A[i]
- Dy[i][1] = (i - 1) 번째 계단에서 이전 계단을 밟지 않은 최대 점수 + A[i]
따라서 구해낸 점화식은 아래와 같다.
1
2
Dy[i][0] = Math.max(Dy[i-2][0], Dy[i-2][1]) + A[i];
Dy[i][1] = Dy[i-1] + A[i];
이 점화식을 기반으로, Dy 테이블을 채워넣으면 된다.
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| A[i] | 0 | 10 | 20 | 15 | 25 | 10 | 20 |
| Dy[i][0] | 0 | 10 | 20 | 25 | 55 | 45 | 75 |
| Dy[i][1] | 0 | 0 | 30 | 35 | 50 | 65 | 65 |
마지막 계단에서 둘중 최대값을 선택하면 정답이다.
위의 예시에서 따라서 정답은 75가 된다.
연습 문제
- BOJ 1149 - RGB 거리, BOJ 2156 - 포도주 시식, BOJ 2193 - 이친수, BOJ 9465 - 스티커, BOJ 1309 - 동물원, ,BOJ 2688 - 줄어들지 않아
두 번째 예시 문제를 살펴보자.
이 문제 또한 가짜 문제를 정의할 때, 길이만 가지고는(1차원 배열) 작은 문제로 큰 문제를 풀 수 없다.
1. 가짜 문제 정의
- 진짜 문제
- 길이가 N인 오르막 수의 개수
- 가짜 문제
Dy[i]: 길이가 i 인 오르막 수의 개수
2. 풀 수 있는가?
Dy[N] 이 곧 정답이 될 것이다.
3. 초기값
Dy[1] = 10; (0~9까지의 숫자)
4. 점화식
여기에서 문제가 발생한다.
이전 단계에서 어떤 숫자를 사용했고, 그 숫자를 사용했을 때 오르막 수의 개수에 대한 정보가 없기 때문에 점화식을 세울수가 없다.
해당 정보를 포함해서 다시 가짜 문제를 정의해보자.
1. 가짜 문제 정의
- 진짜 문제
- 길이가 N인 오르막 수의 개수
- 가짜 문제
Dy[i][j]: 길이가 i 이고 마지막 숫자가 j 인 오르막 수의 개수
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Dy[i][0] | ? | ? | ? | ? | ? | ? | ? |
| Dy[i][1] | ? | ? | ? | ? | ? | ? | ? |
| … | |||||||
| Dy[i][9] | ? | ? | ? | ? | ? | ? | ? |
2. 풀수 있는가?
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Dy[i][0] | ? | ? | ? | ? | ? | ? | X |
| Dy[i][1] | ? | ? | ? | ? | ? | ? | Y |
| … | |||||||
| Dy[i][9] | ? | ? | ? | ? | ? | ? | Z |
Dy 테이블을 다 채우면 마지막 열에 있는 모든 값을 다 더하면 진짜 문제의 정답이 된다.
3. 초기값
길이가 1인 오르막수의 경우, 모든 마지막 숫자에 대해 개수는 1개 뿐이다.
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Dy[i][0] | 1 | ? | ? | ? | ? | ? | ? |
| Dy[i][1] | 1 | ? | ? | ? | ? | ? | ? |
| … | |||||||
| Dy[i][9] | 1 | ? | ? | ? | ? | ? | ? |
4. 점화식
점화식을 세워보자.
Dy[i][j] 를 구하기 위해서는 그 전 까지의 오르막 수 중 마지막 숫자가 j 이하인 경우의 수를 모두 합산하면 된다.
따라서 점화식은 다음과 같이 완성된다.
$Dy[i][j] = \displaystyle\sum_{k=0}^j Dy[i-1][k]$
이를 기반으로 Dy 테이블을 채우면 다음과 같다.
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Dy[i][0] | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| Dy[i][1] | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Dy[i][1] | 1 | 3 | 6 | 10 | 15 | 21 | 28 |
| Dy[i][1] | 1 | 4 | 10 | 20 | 35 | 56 | 84 |
| Dy[i][1] | 1 | 5 | 15 | 35 | 70 | 126 | 210 |
| Dy[i][1] | 1 | 6 | 21 | 56 | 126 | 252 | 462 |
| Dy[i][1] | 1 | 7 | 28 | 84 | 210 | 462 | 924 |
| Dy[i][1] | 1 | 8 | 36 | 120 | 330 | 792 | 1716 |
| Dy[i][1] | 1 | 9 | 45 | 165 | 495 | 1287 | 3003 |
| Dy[i][1] | 1 | 10 | 55 | 220 | 715 | 2002 | 5005 |
따라서 진짜 문제의 정답은 $1 + 7 + 28 + 84 + 210 + 462 + 924 + 1716 + 3003 + 5005 = 11440$ 을 10007로 나눈 나머지인 1433 이 된다.
연습 문제
DP 심화유형
새로운 예시문제를 살펴보자.
이 문제는 여태 풀던 방식으로는 쉽게 풀이가 가늠이 안된다.
시작점을 매번 처음부분 부터 정한 것과는 다르게, 이번에는 특정 위치 i 를 시작점으로 사용해보자.
1. 가짜 문제 정의
- 진짜 문제
- 1 ~ K 번째 파일을 합치는 최소 비용
- 가짜 문제
Dy[i][j]: i ~ j 번째 파일을 합치는 최소 비용
| Dy | j = 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| i = 1 | ? | ? | ? | ? |
| 2 | - | ? | ? | ? |
| 3 | - | - | ? | ? |
| 4 | - | - | - | ? |
2. 풀수 있는가?
Dy 테이블을 다 채우면 Dy[1][K] 가 곧 정답이 된다.
3. 초기값
시작 위치와 끝 위치가 같은 부분은 합치지 않는다. 이 부분은 0 의 값을 가진다.
| Dy | j = 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| i = 1 | 0 | ? | ? | ? |
| 2 | - | 0 | ? | ? |
| 3 | - | - | 0 | ? |
| 4 | - | - | - | 0 |
4. 점화식
점화식을 세워보자.
4-1) 공통점 묶어내기(Partitioning)
구간의 마지막 요소가 어떤 구간으로 계산되는가로 파티션을 묶을수가 있다.(발견하기 쉽지 않다…)
이러한 파티션을 기준으로 점화식을 구해보자.
4-2) 점화식 구하기
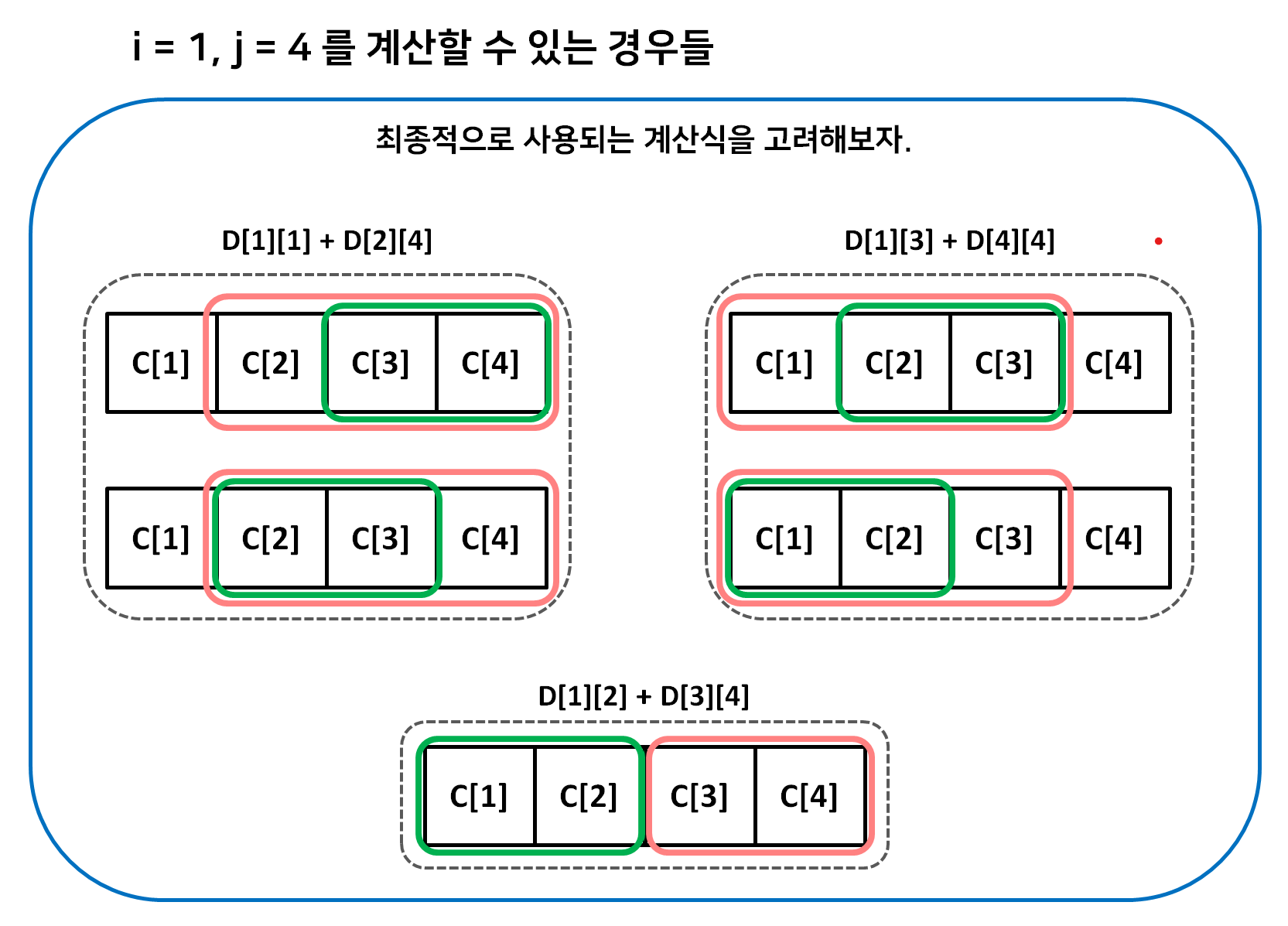
최종적으로 계산되는 구간에 따른 파티션 중 최소값을 찾아내면 된다.
따라서 점화식은 아래와 같다.
\[Dy[i][j] = \displaystyle\min_{i \le x \le j} \lbrace Dy[i][x] + Dy[x + 1][j] \rbrace + \displaystyle\sum_{y=i}^j C[y]\]파티션의 최소 비용을 찾은 후에, 최종적으로 합쳐질 때의 가산 비용인 전체 파일의 크기 합을 더해준다.
Dynamic Table 채우기
이전까지의 문제에선 앞에서부터 순서대로 채우면 문제될 게 없었다.
이번에도 그렇게 하면 될까? 예를 들어 Dy[1][1] 부터 순서대로 Dy[1][2], Dy[1][3], Dy[1][4] 를 채운다고 가정해보자.
이 경우, Dy[1][1] 과 Dy[1][2] 까지는 문제없이 채울 수 있다.
다음으로 Dy[1][3] 을 채울때가 문제인데, 최소값을 찾기위한 파티션들 중 $Dy[1][1] + Dy[2][3]$ 에 필요한 Dy[2][3] 이 채워져있지 않기 때문이다.
이러한 현상이 발생하는 이유는 바로 Dynamic Table 의 짧은 구간부터 채우지 않았기 때문이다.
점화식을 근본적으로 생각해보면, 작은 구간을 활용해 큰 구간을 채워나가는 형태이다. 이 때문에 작은 구간부터 순서대로 모두 채워넣어야 한다.
따라서 이 문제의 경우 Dynamic Table 을 채우는 순서를 살펴보면 다음과 같이 우하향하는 순서로 채워넣은 된다는 것을 볼 수 있다.
| Dy | j = 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| i = 1 | 길이: 1 | 길이: 2 | 길이: 3 | 길이: 4 |
| 2 | - | 길이: 1 | 길이: 2 | 길이: 3 |
| 3 | - | - | 길이: 1 | 길이: 2 |
| 4 | - | - | - | 길이: 1 |
이제 문제 풀이에 필요한 정보는 다 주어졌다.
이전까지와는 관점을 달리 보아야 하는 문제라서 풀기 어려웠지만 많이 풀다보면 익숙해지지 않을까?
연습 문제
다음은 트리에 DP를 적용하는 문제이다.
이러한 subtree 문제는 작은 문제로 큰 문제를 푸는 방식을 적용하기 아주 좋은 예시이다.
자식 노드의 subtree 를 사용해서 부모 노드의 subtree 의 결과값을 얻을 수 있기 때문이다.
그럼 이제 DP 과정을 수행해보자.
1. 문제 정의
Dy[i] : i 가 루트 노드인 subtree 의 정점의 개수
2. 풀 수 있는가?
Dy[루트노드] 값이 곧 답이 된다.
3. 초기값
단말 노드가 곧 초기값이 된다. 단말 노드의 subtree 의 정점은 자기 자신밖에 없으므로 1이 된다.
4. 점화식 구하기
부모 자식 관계를 사용해서 구해낸다.
$Dy[부모 노드] = \sum Dy[자식 노드]$
이전의 문제의 경우 for 반복문을 사용하여 차례차례 Dynamic Table 을 채워나갔다면, 이 문제는 트리 구조의 탐색에 사용한 dfs 를 활용하여 채워나간다.
따라서 시간복잡도는 $O(V + E) = O(N)$ 이 된다.
비슷한 문제로 BOJ 1949 - 우수 마을 이 있다.(이 문제의 점화식을 잘 생각해보자. 풀이를 보면 되게 쉬운데 떠올리기까지가 힘들다. 이전의 subtree 점화식에 특정 기준 하나를 더 추가하는데, 문제에서 주어진 조건을 보고 잘 생각해보자.)
번외) 동적프로그래밍의 역추적(Backtrack)
동적 프로그래밍을 정말로 이해했다고 말하기 위해서는 다음 질문에 대해서 대답할 수 있어야 한다고 한다.
- BOJ 2579 - 계단 오르기 문제에서 최대값은 알겠는데, 실제로 어떻게 이동해야 최대값이 나오는가?
이 질문에 대답하기 위해서는 Dy 테이블을 채워나갈 때에 기록을 함께 해야한다.
자세히 설명하자면, Dy[i][0] 을 채울 때 Before[i][0] 에는 $max(Dy[i-2][0], Dy[i-2][1])$ 에 따라 [i-2, 0] 혹은 [i-2][1] 을 저장하고, dy[i][1] 을 채울 때는 Before[i][1] 에는 [i - 1, 0] 을 저장하는 식이다.
이런식으로 Dy 테이블을 채워나갈 때, 어디서 값을 가져와서 채웠는지에 대한 기록을 함께 해주면 정답을 구하는 실제 방법도 알 수 있는데, 이를 역추적(Backtrack) 이라고 한다.