컴퓨터 구조 - 2-2. 데이터의 표현(정수 표현, 실수 표현)

이 포스트는 패스트캠퍼스의 “컴퓨터 공학 전공 필수 올인원 패키지 Online.” 강의를 보고 정리한 내용입니다.

데이터의 표현

컴퓨터에서 데이터를 표현하는 방법에 대해서 알아보자.

1. 정수 표현

정수형이란, 소숫점이 고정되어있는 수(고정 소숫점, Fixed Point Number)를 뜻한다.

1-1. 부호화 절대치(Signed Magnitude)

정수의 양수와 음수를 표현하기 위해 정수의 부호와 절대치를 따로 보관하는데, 가장 왼쪽의 bit 를 부호를 표현하는 sign bit 로서 사용하고, sign bit 가 0 이면 양수, 1 이면 음수로 사용한다.

따라서 N bit 를 사용하는 2진수의 경우, 표현 범위는 $-(2^{n-1} - 1)$ ~ $(2^{n-1} - 1)$ 이 된다.

분수의 표현같은 컴퓨터의 특성상 딜레마들 중 하나로 +0 과 -0 이 공존한다.

이런 문제를 해결하기 위해 Two’s Complement 를 채택하게 되는데, 달라지는 점은 다음과 같다.

4 bit 짜리 2진수 A 가 0000 이라고 가정했을 때, 2의 보수는 $1111 + 1 = 10000$ 이 되는데, 4 bit 로는 똑같이 0000 으로 표현이 되므로, 0 은 무조건 0000 으로 표현이 통일되어 +0 과 -0 이 공존하는 모순을 해결한다.

1의 보수에서 -0 으로 사용되던 1000 은 2의 보수에서 $-2^{n-1}$ 의 음수를 나타내게 되며, 따라서 표현 범위도 N bit 를 사용한다 가정했을 때 $-2^{n-1}$ ~ $(2^{n-1} - 1)$ 이 된다.

4비트 2진수의 값의 2의 보수를 예시로 살펴보자.

2진수(양수)	2진수(2의 보수)
0000 = 0
0001 = 1	1111 = -1
0010 = 2	1110 = -2
0011 = 3	1101 = -3
0100 = 4	1100 = -4
0101 = 5	1011 = -5
0110 = 6	1010 = -6
0111 = 7	1001 = -7
	1000 = -8

1-2. Unpacked Decimal(Zoned Decimal)

수치형으로 사용되는 정수는 연산을 위해 위의 방식처럼 2로 나누어서 2진법으로 저장한다. 더 큰 10진수 일수록 자릿수가 많아지고 변환에 따른 연산량이 많아진다.

하지만 연산에 사용하지 않는 비 수치 데이터(Alphanumerical data; 입출력용 데이터)의 경우에는 저장을 위해 이러한 연산을 하는게 불필요한 과정이므로, 다른 표현 방식을 사용한다.

사용 방식

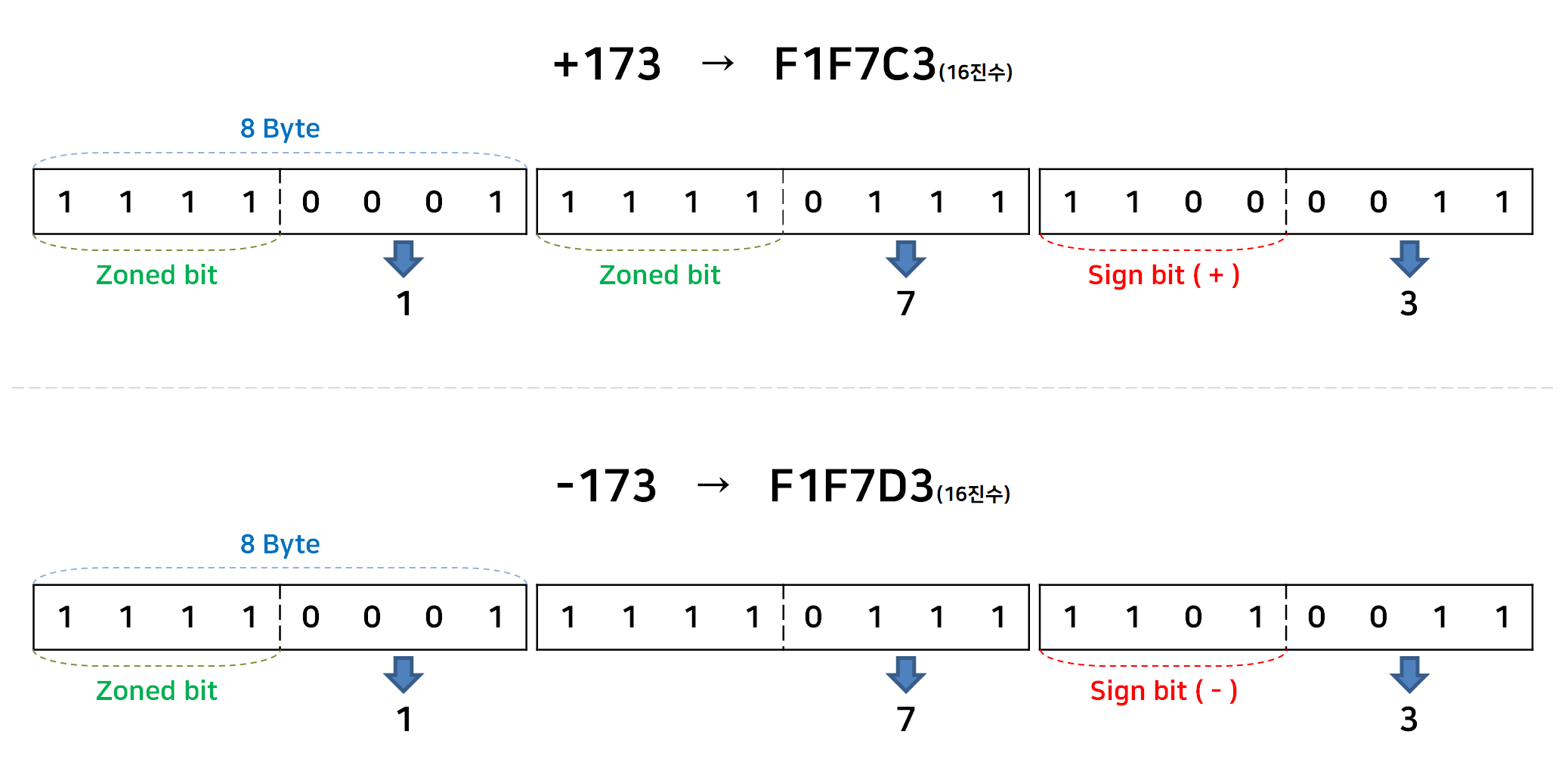
사용 방식은 한 자리의 10진수를 1 Byte 로 표현하는데, 앞의 4 bit 와 뒤의 4 bit 로 나뉜다.

뒤의 4 bit 는 단순히 각 자릿수의 절대치를 나타내는 역할이고, 0 ~ 9 를 표현해야 하므로 4 bit 면 충분한다.

앞의 4 bit 는 Zoned bit 와 Sign bit 두 가지 역할을 가지는데, 마지막 숫자를 나타낼 때 사용되는 앞의 4 bit 만이 Sign bit 로 사용된다.

Sign bit 는 10진수가 양수인지 음수인지 나타내는데, 1100 이면 양수, 1101 이면 음수 를 나타낸다.

마지막 숫자를 제외한 나머지 숫자를 표현할 때 앞의 4 bit는 단순히 Zoned bit 로서 1111 의 고정값을 가진다.

예시) 10진수 173 과 -173 을 표현하는 방법은 다음과 같다.

이러한 형태를 연산에는 사용할 수 없지만 간편하게 입출력에 사용할 수 있다.

IBM 에서 사용되던 EBCDIC 의 숫자 표현과 동일한 방식이다.

1-3. Packed Decimal

Unpacked Decimal 을 연산에 사용하기 위해 Packed Decimal 로 변환하여 사용하기도 한다.

사용 방식

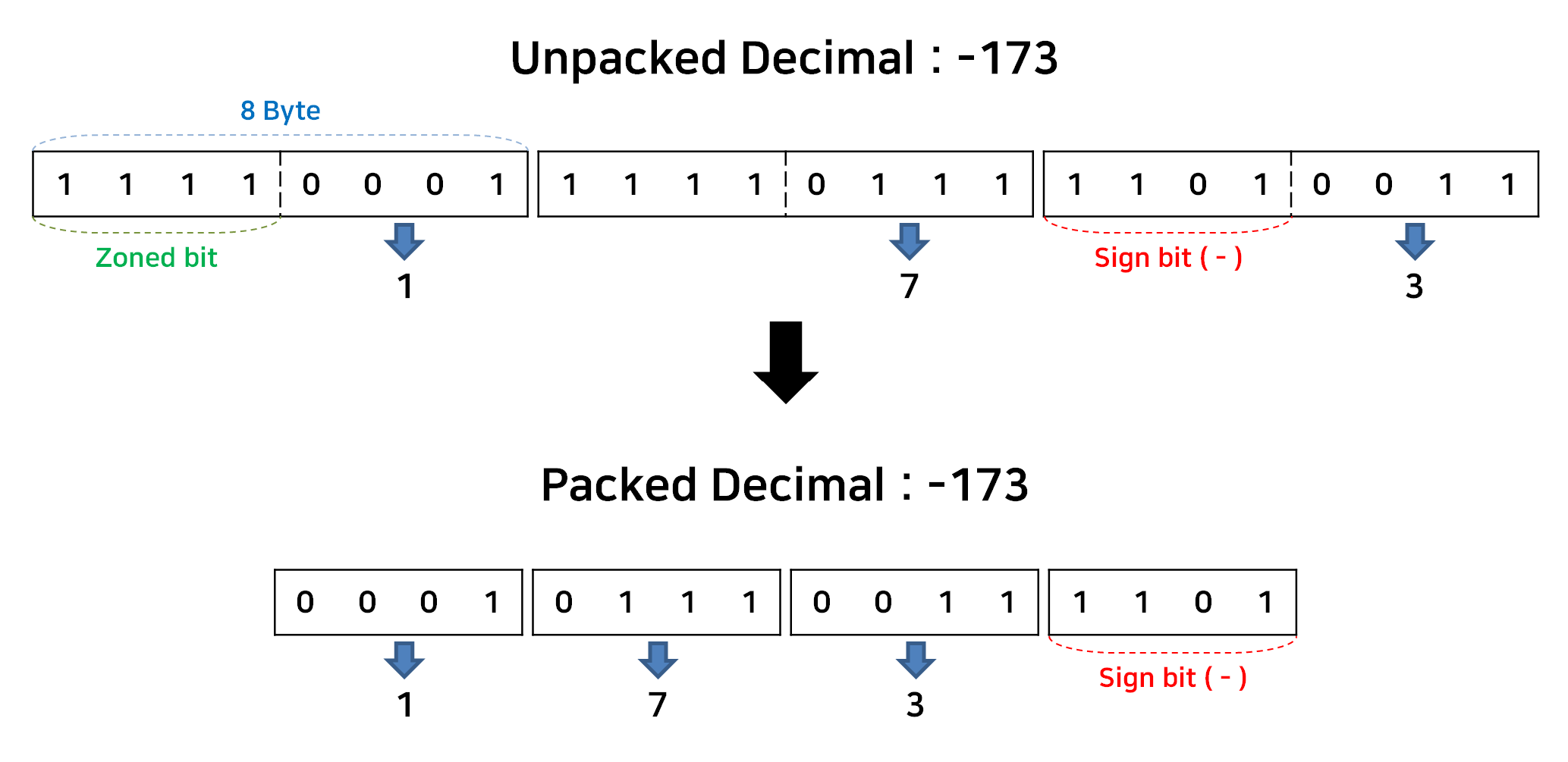
Packed Decimal 의 Sign bit 를 맨 뒤로 미룬 후 절대치들만 모두 앞으로 가져와서 사용한다. Zoned bit 는 생략한다.

예시) Unpacked Decimal -173 을 Packed Decimal 로 변환하자.

변환된 결과는 연산에는 사용이 가능하지만, 입출력에는 사용이 불가능하다.

---

2. 실수 표현

실수형이란, 과학적 표기인 지수(exponent) 형태를 사용하여 소수점의 위치를 이동시키는 표현 형태(부동 소수점, Floating-point)이다.

이러한 실수형은 비트 수에 따른 분류가 가능하다.

2-1. 단일 정밀도 부동 소수점 형식(Single-Precision Floating Point)

예를들어 32비트의 실수 형식인 단일 정밀도 부동 소수점 형식을 알아보자.

IEEE 754 표준에 정의된 binary32 형식의 사용 방법은 다음과 같다.

1. 실수값은 2진수로 표현한다.
2. 표현된 2진수값을 (1.XXXX) 형태로 정규화한다.
   • 이 때, 정규화에 사용된 지수값에 편향값인 127을 더한다.
3. 정규화된 값을 다음과 같은 3가지 부분으로 저장한다.
   • 첫번째 비트는 부호를 나타내는 부호(Sign) 비트로 사용한다.
     • 0: 양수(+), 1: 음수(-)
   • 다음 8비트는 지수를 나타내는 지수(Exponent) 비트로 사용된다.
     • 표준에 정의된 binary32 형식은 bias127, 즉 지수부의 편향값으로 127을 사용한다.
     • 실제 지수값 + 127 을 2진수값으로 저장한다.
   • 나머지 23비트는 가수를 나타내는 가수(Fraction) 비트로 사용된다.
     • 실제 값을 나타내는 부분이 된다.
     • 정규화된 값에서 앞의 1. 을 제외한 뒷부분

이를 간단한 예시로 살펴보면 다음과 같다.

실수값 저장

먼저, 실수값을 저장하기위해 변환하는 과정을 보자.

실수값 15.6875 을 저장한다고 가정하자.

이를 이진수값으로 표현하면 다음과 같다.

$15.6875 = 1111.1011_{(2)}$

이를 정규화하면 다음과 같은 지수값을 얻을 수 있다.

$1111.1011_2 = 1.1111011_2 * 2^3$

따라서 실제 저장은 다음과 같이 한다.

• 부호 비트 : 양수이므로 0
• 지수부 : $3 + 127 = 130 = 10000010_{(2)}$
• 가수부 : $1111 0110 0000 0000 0000 000_{(2)}$

저장된 값 실수화

다음은 저장된 값을 실제 실수값으로 변환하는 과정이다.

지수부에 저장된 값은 실제 지수값이 아닌 편향값인 127을 더한 값이 저장된다. 따라서 위 예시의 실제 지수값은 저장된 값에 편향값인 127을 뺀 값이다.

실제 지수값 : $10000010_{(2)} - 127 = 130 - 127 = 3$

따라서 가수부에 저장된 값에 $2^3$ 만큼을 곱해주면 원래 실수값을 구할 수 있다.

실제 실수값 : $1.F_2 * 2^{E} = 1.10011000001_2 * 2^3 = 1100.11000001_2 = 12.75390625$

F : 가수, E : 지수

이러한 표준은 C, C++, C#, Java 언어에서 float 라는 타입명으로 사용된다.